Điện thoại
Laptop
Phụ kiện
Smartwatch
Đồng hồ
Tablet
Máy cũ, Thu cũ
Màn hình, Máy in
Sim, Thẻ cào
Dịch vụ tiện ích
Giải thuật là gì?
Giải thuật (hay còn gọi là thuật toán - tiếng Anh là Algorithms) là một tập hợp hữu hạn các chỉ thị để được thực thi theo một thứ tự nào đó nhằm thu được kết quả mong muốn.
Nói một cách ngắn gọn, giải thuật là tập hợp các bước, thao tác để giải quyết một vấn đề gì đó.
Giải thuật là tập hợp các thao tác để giải quyết vấn đề
Giả sử như bạn có một vấn đề cần giải quyết đó là biến gạo thành cơm để ăn (hay nói cách khác là nấu cơm), bạn sẽ phải thực hiện những bước sau đây:
Giải thuật là độc lập với các ngôn ngữ lập trình, tức là một giải thuật có thể được triển khai trong nhiều ngôn ngữ lập trình khác nhau.
Không phải tất cả các thủ tục đều được gọi là một giải thuật. Một giải thuật nên có các đặc điểm sau:
Giải thuật dừng lại sau 1 số bước nhất định
Cấu trúc dữ liệu và giải thuật rất quan trọng trong lập trình, không riêng ngôn ngữ Java, PHP, Python.. tất cả ngôn ngữ lập trình khác điều cần cấu trúc dữ liệu và giải thuật.
Việc chuyển đổi ngôn ngữ lập trình không quá khó. Thứ quyết định và sẽ đi theo bạn là cấu trúc dữ liệu và giải thuật. Việc sở hữu một tư duy giải thuật sẽ giúp bạn hoàn thành tốt các công việc lập trình.
1. Ngôn ngữ viết
Thiết kế giải thuật bằng ngôn ngữ viết là liệt kê tuần tự các bước bằng ngôn ngữ tự nhiên để biểu diễn thuật toán.
Ưu điểm:
Đơn giản, không cần kiến thức về cách biểu diễn (mã giả, lưu đồ,...)
Nhược điểm:
Ví dụ: Dùng ngôn ngữ viết để tìm ra 3 số lớn nhất trong a, b, c
2. Lưu đồ
Lưu đồ bao gồm:
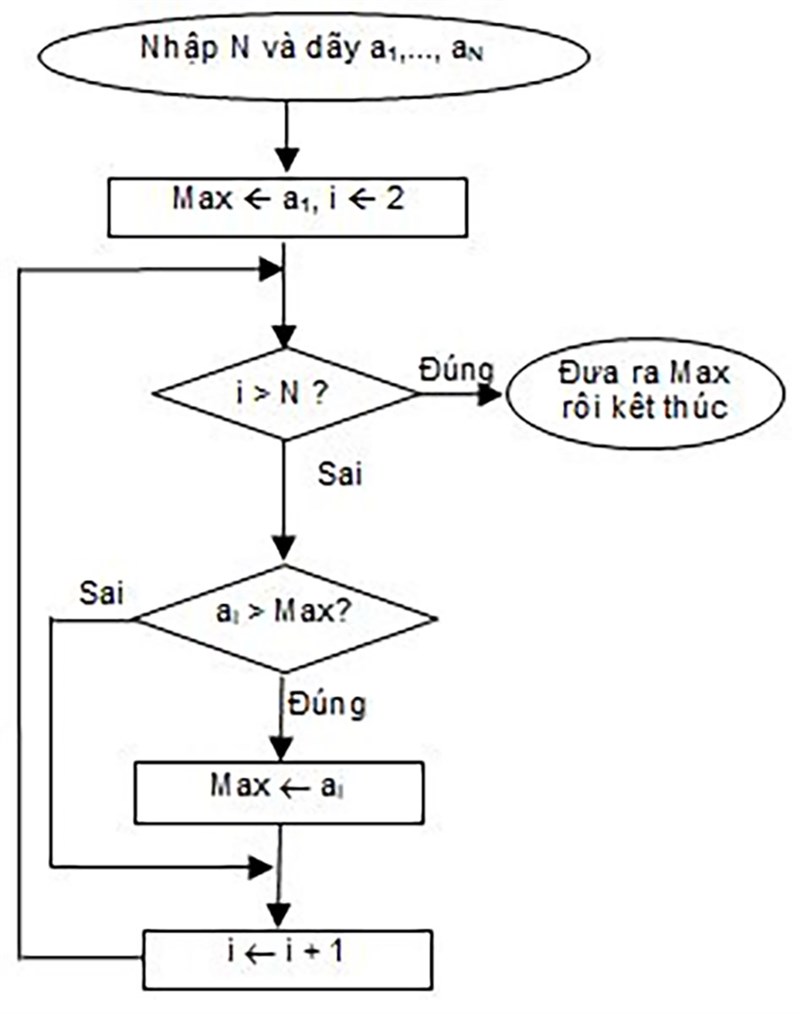
Lưu đồ
Ưu điểm:
Trực quan, dễ hình dung.
Nhược điểm:
Cồng kềnh nếu vấn đề xử lý quá phức tạp.
3. Mã giả
Ngôn ngữ của mã giả khá giống ngôn ngữ lập trình. Nó thường dùng cấu trúc chuẩn hóa, chẳng hạn tựa Pascal, C. Nó cũng sử dụng các ký hiệu toán học, biến, hàm.
Một mã giả
Ưu điểm:
Không cồng kềnh như lưu đồ khối
Nhược điểm:
Không trực quan bằng lưu đồ khối.
4. Ngôn ngữ lập trình
Viết "Hello world" bằng ngôn ngữ Java
1. Vì sao cần phản phân tích giải thuật
Trong khi giải một bài toán chúng ta có thể có một số giải thuật khác nhau, vấn đề là cần phải đánh giá các giải thuật đó để lựa chọn một giải thuật tốt nhất.
2. Phân tích lý thuyết
Có thể coi đây là phân tích chỉ dựa trên lý thuyết. Hiệu quả của giải thuật được đánh giá bằng việc giả sử rằng tất cả các yếu tố khác (ví dụ: tốc độ vi xử lý, …) là hằng số và không ảnh hưởng tới sự triển khai giải thuật.
3. Phân tích tiệm cận:
Việc phân tích giải thuật này được tiến hành sau khi đã tiến hành trên một ngôn ngữ lập trình nào đó.
Sau khi chạy và kiểm tra đo lường các thông số liên quan thì hiệu quả của giải thuật dựa trên các thông số như thời gian chạy, thời gian thực thi, lượng bộ nhớ cần dùng, …
1. Độ phức tạp của giải thuật là gì?
Độ phức tạp giải thuật là một hàm ước lượng (có thể không chính xác) số phép tính mà giải thuật cần thực hiện (từ đó dễ dàng suy ra thời gian thực hiện của giải thuật) đối với bộ dữ liệu đầu vào (Input) có kích thước n.
Trong đó, n có thể là số phần tử của mảng trong trường hợp bài toán sắp xếp hoặc tìm kiếm, hoặc có thể là độ lớn của số trong bài toán kiểm tra số nguyên tố, …
Giả sử X là một giải thuật và n là kích cỡ của dữ liệu đầu vào. Thời gian và lượng bộ nhớ được sử dụng bởi giải thuật X là hai nhân tố chính quyết định hiệu quả của giải thuật X:
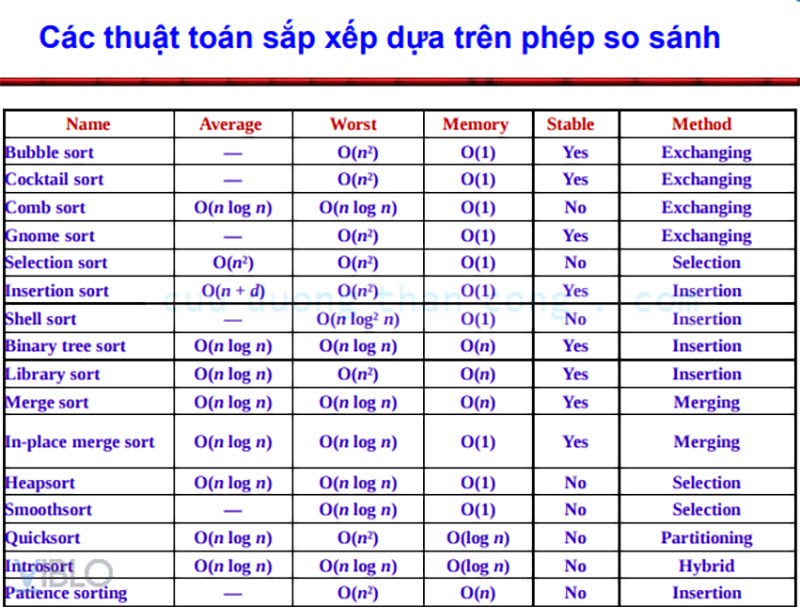
Các phép so sánh trong thuật toán sắp xếp
Độ phức tạp của một giải thuật (một hàm f(n)) cung cấp mối quan hệ giữa thời gian chạy và/hoặc lượng bộ nhớ cần được sử dụng bởi giải thuật.
2. Độ phức tạp bộ nhớ trong phân tích giải thuật (Space complexity)
Nhân tố bộ nhớ của một giải thuật biểu diễn lượng bộ nhớ mà một giải thuật cần dùng trong vòng đời của giải thuật.
Lượng bộ nhớ (giả sử gọi là S(P)) mà một giải thuật cần sử dụng là tổng của hai thành phần sau:
Từ trên, ta sẽ có S(P) = C + SP(I). Bạn theo dõi ví dụ đơn giản sau:
Ở đây chúng ta có ba biến A, B và C và một hằng số. Do đó: S(P) = 1+3.
Bây giờ, lượng bộ nhớ sẽ phụ thuộc vào kiểu dữ liệu của các biến và hằng đã cho và sẽ bằng tích của tổng trên với bộ nhớ cho kiểu dữ liệu tương ứng.
3. Độ phức tạp thời gian trong phân tích giải thuật (Time Complexity)
Nhân tố thời gian của một giải thuật biểu diễn lượng thời gian chạy cần thiết từ khi bắt đầu cho đến khi kết thúc một giải thuật.
Thời gian yêu cầu có thể được biểu diễn bởi một hàm T(n), trong đó T(n) có thể được đánh giá như là số các bước.
Ví dụ, phép cộng hai số nguyên n-bit sẽ có n bước. Do đó, tổng thời gian tính toán sẽ là T(n) = c*n
Trong đó c là thời gian để thực hiện phép cộng hai bit. Ở đây, chúng ta xem xét hàm T(n) tăng tuyến tính khi kích cỡ dữ liệu đầu vào tăng lên.
Xem thêm:
Trên đây là khái niệm về giải thuật và cách thiết kế giải thuật đơn giản, dễ hiểu. Hi vọng bài viết này sẽ giúp ích cho bạn. Đừng quên chia sẻ bài viết nếu thấy hữu ích nhé!
↑
Xóa địa chỉ
Có
ĐĂNG NHẬP
Hãy đăng nhập để Chia sẻ bài viết, bình luận, theo dõi các hồ sơ cá nhân và sử dụng dịch vụ nâng cao khác trên trang Game App của
Thế Giới Di Động
Tất cả thông tin người dùng được bảo mật theo quy định của pháp luật Việt Nam. Khi bạn đăng nhập, bạn đồng ý với Các điều khoản sử dụng và Thoả thuận về cung cấp và sử dụng Mạng Xã Hội.