Tham khảo ngay một số mẫu điện thoại thông minh GIẢM SỐC đang kinh doanh tại Thế Giới Di Động:
Trực tâm là một trong những khái niệm quan trọng và cơ bản nhất trong hình học phẳng, đặc biệt là với các bạn học sinh. Việc hiểu rõ trực tâm không chỉ giúp giải quyết các bài toán mà còn mở ra những ứng dụng thú vị trong đời sống. Khám phá ngay tất cả kiến thức về trực tâm của tam giác!
1. Trực tâm là gì?
Trực tâm là một trong bốn điểm đặc biệt của tam giác, bên cạnh trọng tâm, tâm đường tròn nội tiếp và ngoại tiếp.
Trực tâm là giao điểm của ba đường cao trong một tam giác. Trong đó, đường cao là đoạn thẳng kẻ từ một đỉnh và vuông góc với cạnh đối diện. Mỗi tam giác luôn có ba đường cao. Trong toán học, trực tâm thường được ký hiệu là điểm H.

Trực tâm là giao điểm của ba đường cao trong một tam giác
2. Vị trí của trực tâm trong các loại tam giác
Không giống như trọng tâm luôn nằm trong tam giác, vị trí của trực tâm có thể thay đổi tùy thuộc vào đặc điểm các góc của tam giác đó.
Đối với tam giác nhọn
Tam giác nhọn là tam giác có cả ba góc đều nhỏ hơn 90 độ. Lúc này, ba đường cao đều nằm hoàn toàn bên trong tam giác. Do đó, đối với tam giác nhọn, trực tâm nằm bên trong tam giác.

Đối với tam giác nhọn, trực tâm nằm bên trong tam giác
Đối với tam giác vuông
Tam giác vuông có một góc bằng 90 độ. Hai cạnh góc vuông chính là hai đường cao của tam giác. Đường cao thứ ba xuất phát từ đỉnh góc vuông. Vì vậy, đối với tam giác vuông trực tâm trùng với đỉnh góc vuông.
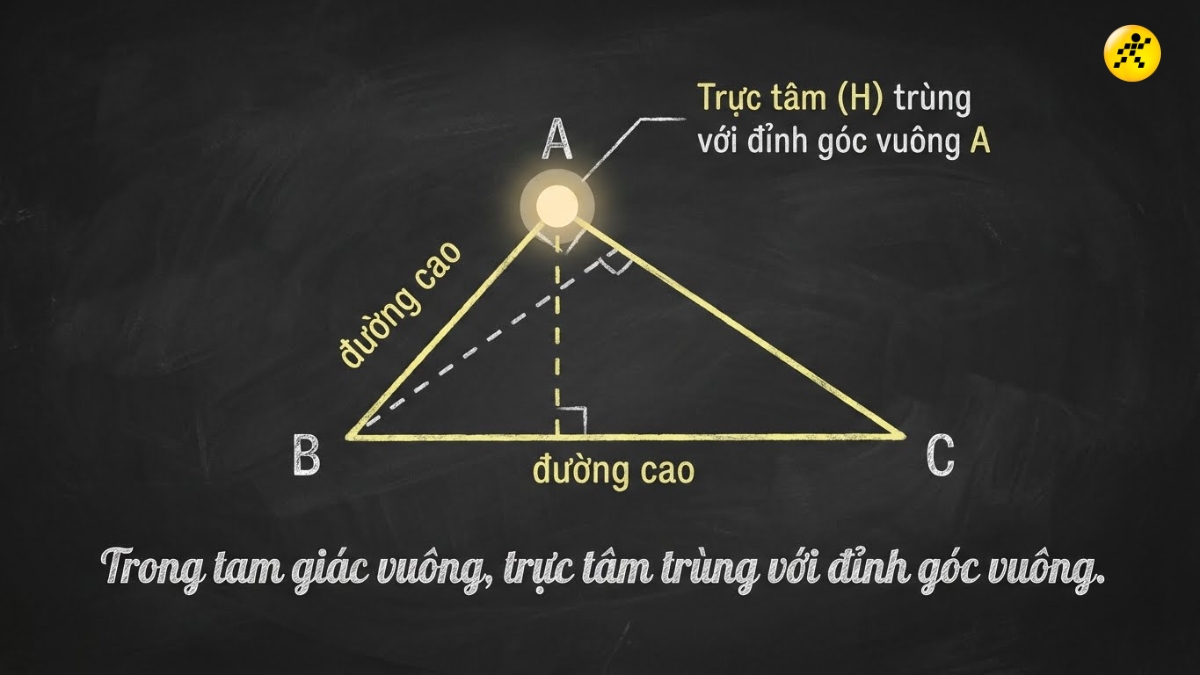
Đối với tam giác vuông trực tâm trùng với đỉnh góc vuông
Đối với tam giác tù
Tam giác tù có một góc lớn hơn 90 độ. Để kẻ đường cao từ hai đỉnh góc nhọn, ta phải kéo dài các cạnh đối diện. Giao điểm của ba đường cao sẽ nằm ở phía ngoài. Kết luận: Đối với tam giác tù, trực tâm nằm bên ngoài tam giác.
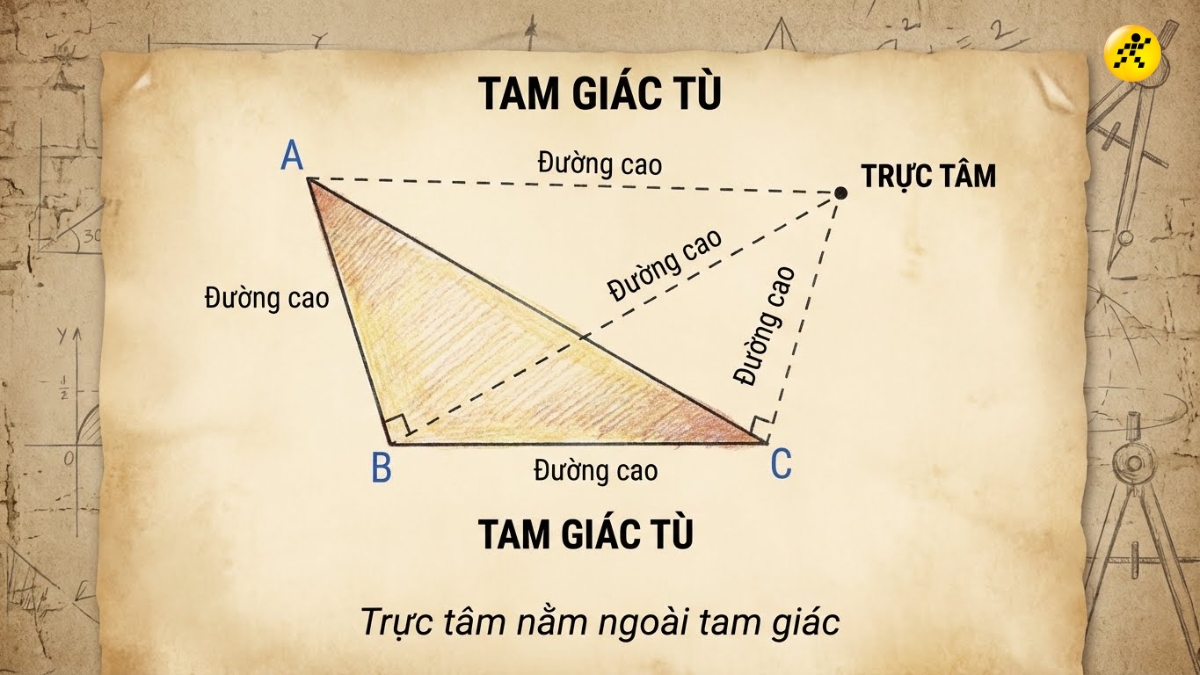
Đối với tam giác tù, trực tâm nằm bên ngoài tam giác
3. Các tính chất quan trọng của trực tâm
Trực tâm không chỉ là một điểm giao nhau đơn thuần mà còn mang nhiều tính chất hình học quan trọng, giúp ích cho việc chứng minh và giải các bài toán phức tạp.
Tính chất đồng quy
Đây là tính chất cơ bản nhất: Ba đường cao của một tam giác luôn cùng đi qua một điểm, điểm đó chính là trực tâm.
Mối quan hệ với các điểm đặc biệt khác
- Trong tam giác đều: Trực tâm, trọng tâm, tâm đường tròn ngoại tiếp, tâm đường tròn nội tiếp là trùng nhau.
- Trong tam giác thường: Ba điểm trực tâm (H), trọng tâm (G) và tâm đường tròn ngoại tiếp (O) cùng nằm trên một đường thẳng. Đường thẳng này được gọi là đường thẳng Euler.
- Trong tam giác cân: Trực tâm nằm trên đường trung tuyến ứng với cạnh đáy.
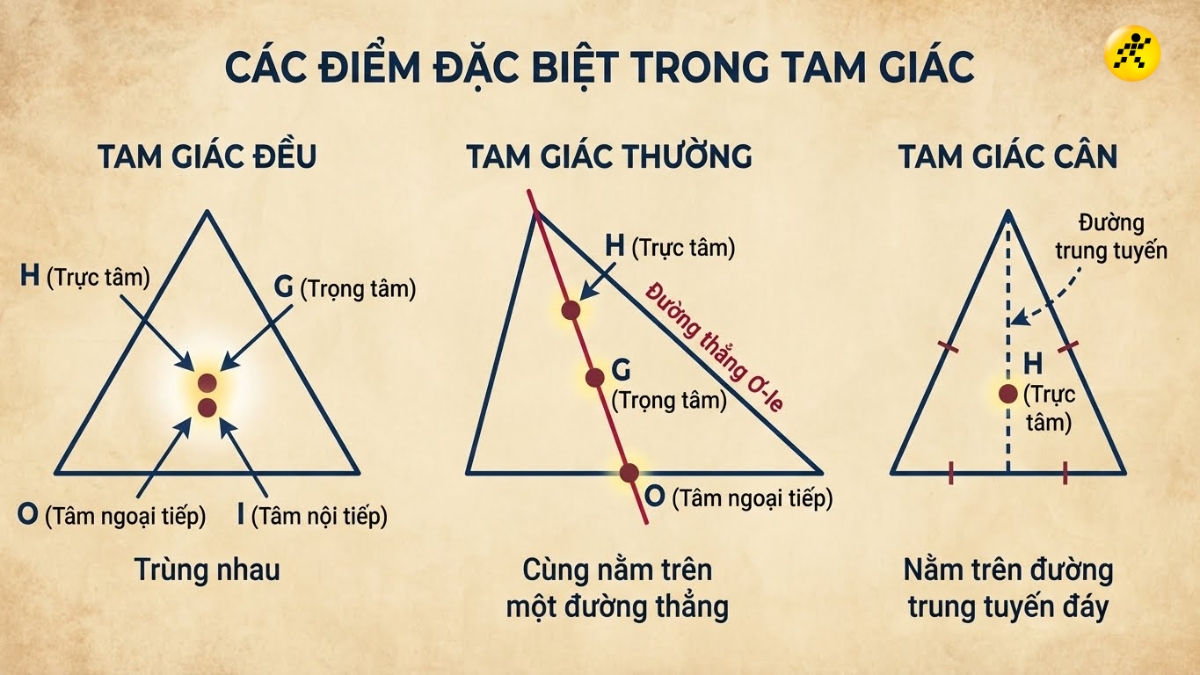
Mối quan hệ với các điểm đặc biệt khác
Lưu ý quan trọng: Đường thẳng Euler là một trong những định lý nổi tiếng của hình học phẳng, thể hiện mối quan hệ thẳng hàng đặc biệt giữa ba điểm quan trọng của tam giác. Đây là một kiến thức nâng cao hữu ích cho các bài toán hình học phức tạp.
4. Cách xác định trực tâm của tam giác
Có hai phương pháp chính để xác định trực tâm: phương pháp dựng hình trực quan và phương pháp tính toán trong hình học giải tích.
Phương pháp hình học (Dùng thước và êke)
Bước 1: Chọn đỉnh thứ nhất (ví dụ đỉnh A), dùng êke đặt một cạnh góc vuông trùng với cạnh đối diện (BC), sau đó kẻ đường thẳng theo cạnh góc vuông còn lại của êke đi qua đỉnh A. Đây là đường cao thứ nhất.
Bước 2: Lặp lại thao tác tương tự với đỉnh thứ hai (ví dụ đỉnh B) để vẽ đường cao thứ hai vuông góc với cạnh AC.
Bước 3: Giao điểm của hai đường cao vừa vẽ chính là trực tâm H của tam giác. Không cần thiết phải vẽ đường cao thứ ba vì ba đường cao luôn đồng quy.
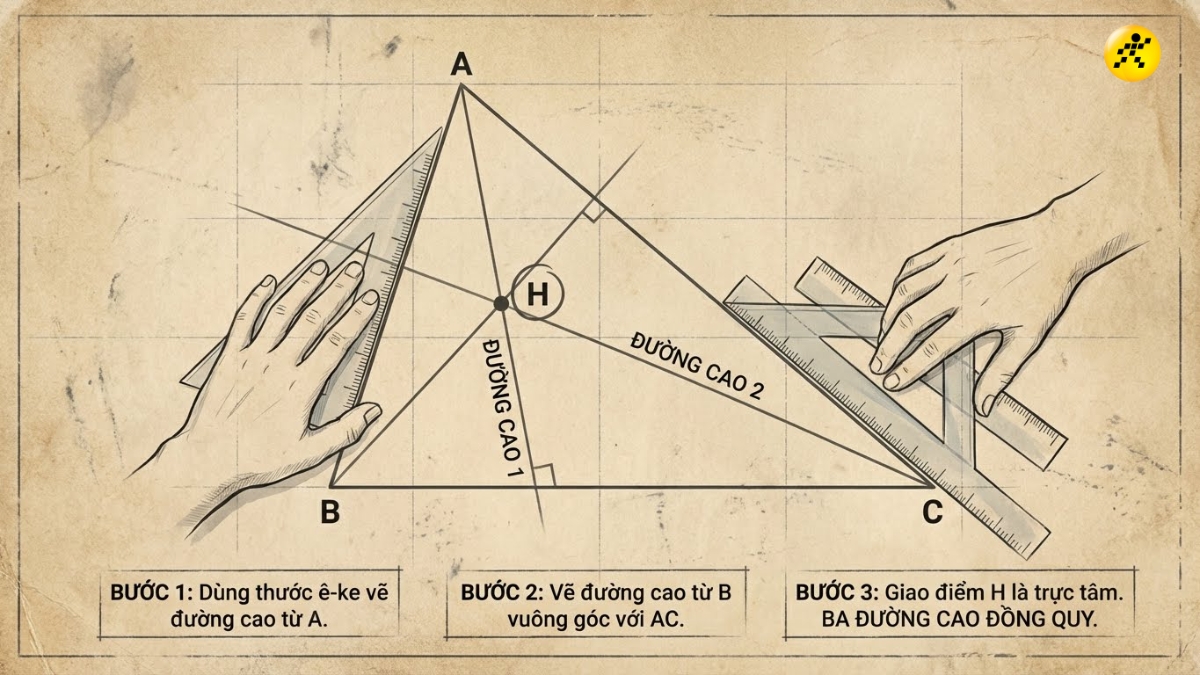
Phương pháp hình học
Phương pháp tọa độ (Trong hình học giải tích)
Bước 1: Tìm vector chỉ phương của các cạnh (ví dụ vectơ BC).
Bước 2: Suy ra vector pháp tuyến của đường cao tương ứng (đường cao từ A sẽ nhận vectơ BC làm vector pháp tuyến).
Bước 3: Viết phương trình đường thẳng của hai đường cao.
Bước 4: Giải hệ phương trình của hai đường thẳng đó để tìm tọa độ giao điểm, đó chính là tọa độ trực tâm.
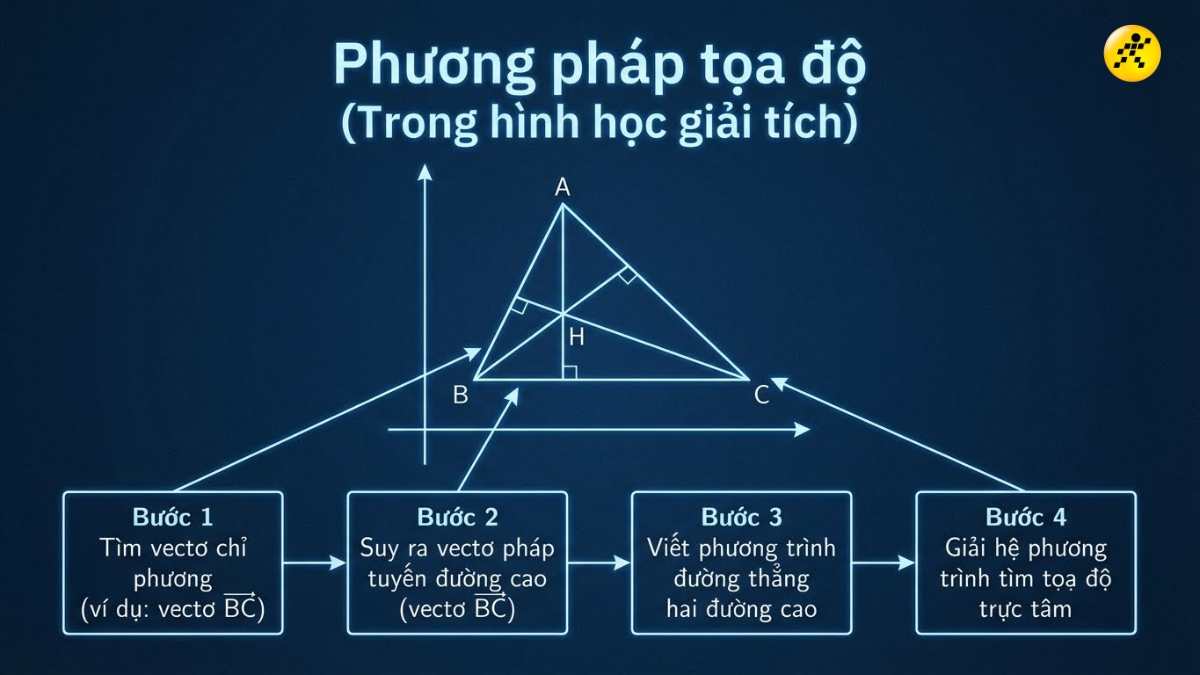
Phương pháp tọa độ
5. Ứng dụng của trực tâm trong thực tế
Dù là một khái niệm toán học trừu tượng, nguyên lý về trực tâm và đường cao lại có những ứng dụng đáng ngạc nhiên trong nhiều lĩnh vực từ kỹ thuật đến công nghệ hiện đại.
Trong xây dựng và kiến trúc
Các kỹ sư sử dụng các nguyên lý tương tự để xác định các điểm chịu lực, trọng tâm và các đường giằng vuông góc trong các kết cấu như mái nhà, cây cầu, giàn khoan để đảm bảo sự vững chắc, cân bằng và ổn định.
Trong công nghệ và AI
Các thuật toán nhận diện vật thể trong camera của điện thoại thông minh sử dụng các nguyên lý hình học để xác định hình dạng, trọng tâm và các trục đối xứng của vật thể. Điều này giúp camera lấy nét chính xác hơn, đặc biệt trong chế độ chụp chân dung.
Tương tự, robot sử dụng các cảm biến và thuật toán trí tuệ nhân tạo (AI) để xác định "đường cao" (khoảng cách vuông góc) tới các vật thể, giúp chúng di chuyển và giữ th&ng bằng.
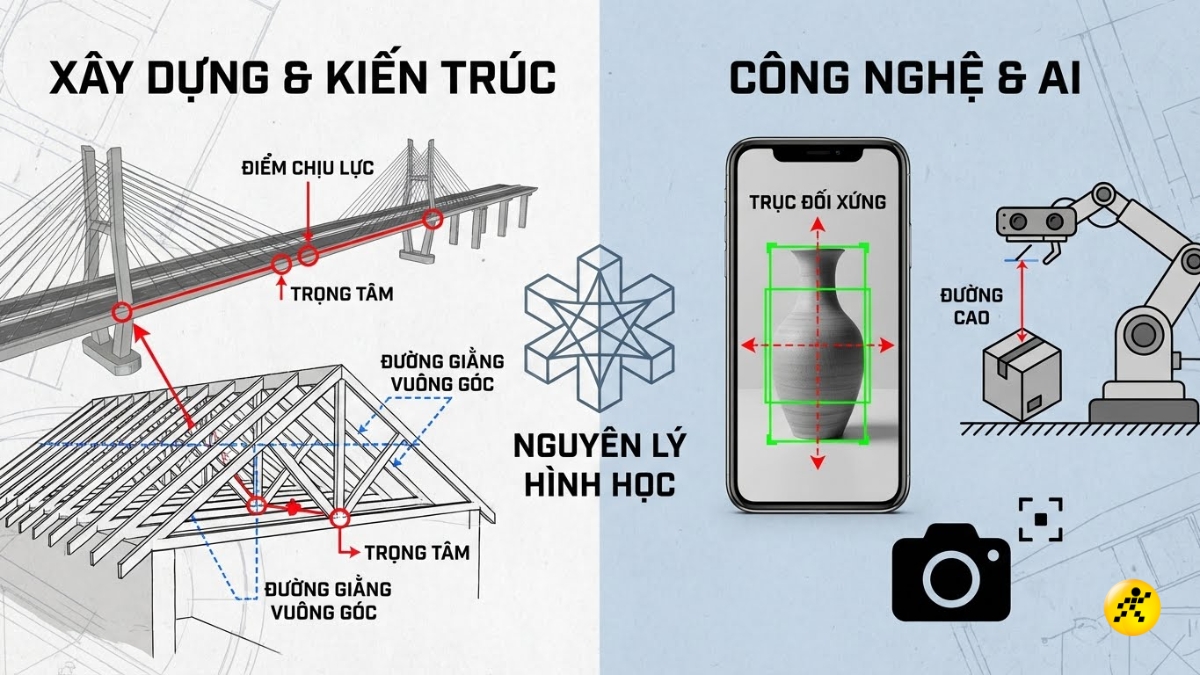
Ứng dụng của trực tâm trong thực tế
Khám phá các mẫu điện thoại với camera AI đỉnh cao:
6. Phân biệt trực tâm, trọng tâm, tâm đường tròn ngoại tiếp và nội tiếp
Việc phân biệt rõ 4 điểm đặc biệt này là cực kỳ quan trọng để tránh nhầm lẫn khi giải toán. Dưới đây là bảng so sánh chi tiết:
|
Tiêu chí
|
Trực tâm
|
Trọng tâm
|
Tâm đường tròn ngoại tiếp
|
Tâm đường tròn nội tiếp
|
|
Định nghĩa
|
Giao điểm 3 đường cao
|
Giao điểm 3 đường trung tuyến
|
Giao điểm 3 đường trung trực
|
Giao điểm 3 đường phân giác
|
|
Tính chất
|
Cách đều 3 đỉnh (sai)
|
Cách đỉnh bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó
|
Cách đều 3 đỉnh của tam giác
|
Cách đều 3 cạnh của tam giác
|
|
Vị trí
|
Trong, ngoài, trên đỉnh tam giác
|
Luôn ở trong tam giác
|
Trong, ngoài, trên cạnh tam giác
|
Luôn ở trong tam giác
|
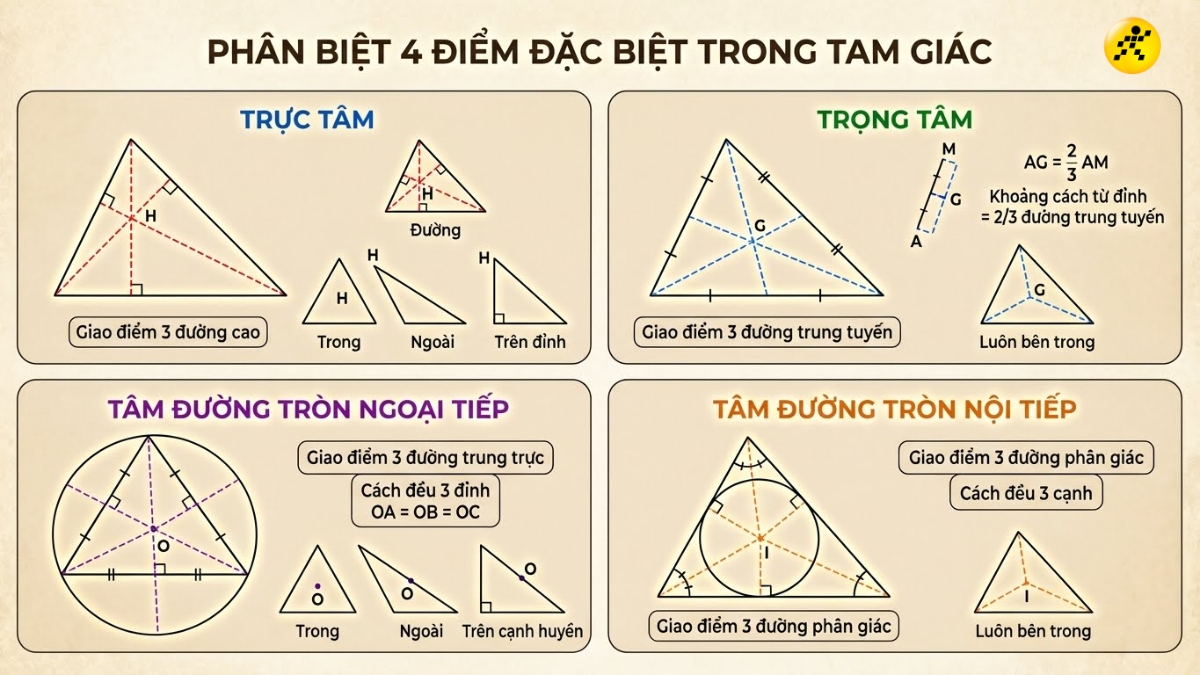
Phân biệt trực tâm, trọng tâm, tâm đường tròn ngoại tiếp và nội tiếp
7. Câu hỏi liên quan
Dưới đây là một số câu hỏi thường gặp giúp bạn củng cố kiến thức về trực tâm:
Trực tâm có phải lúc nào cũng nằm trong tam giác không?
Không, trực tâm chỉ nằm trong tam giác nhọn. Nó nằm ngoài tam giác tù và trùng với đỉnh góc vuông của tam giác vuông.
Tam giác nào có trực tâm trùng với trọng tâm?
Trong tam giác đều, bốn điểm đặc biệt bao gồm trực tâm, trọng tâm, tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp đều trùng nhau tại một điểm.
Đường thẳng Euler là gì?
Đó là đường thẳng đi qua 3 điểm: Trực tâm, trọng tâm và tâm đường tròn ngoại tiếp của một tam giác.
Làm sao để tìm trực tâm nhanh nhất?
Bạn chỉ cần vẽ chính xác 2 trong 3 đường cao của tam giác. Giao điểm của chúng chính là trực tâm.
Trực tâm có ứng dụng gì trong camera điện thoại?
Các nguyên lý hình học liên quan đến trực tâm giúp các thuật toán AI trong camera điện thoại nhận diện và phân tích vật thể, từ đó tối ưu hóa khả năng lấy nét và xử lý hình ảnh.
Hy vọng bài viết đã giúp bạn hiểu rõ "trực tâm là gì" cũng như các tính chất và ứng dụng quan trọng của nó. Việc nắm vững kiến thức này không chỉ cần thiết cho việc học tập mà còn giúp bạn thấy được sự thú vị của toán học trong cuộc sống hàng ngày!
Có thể bạn quan tâm đến các mẫu điện thoại đang được khuyến mãi tại TGDĐ:
 Điện thoại
Điện thoại
 Laptop
Laptop
 Phụ kiện
Phụ kiện
 Smartwatch
Smartwatch
 Đồng hồ
Đồng hồ
 Tablet
Tablet
 Máy cũ, Thu cũ
Máy cũ, Thu cũ
 Màn hình, Máy in
Màn hình, Máy in
 Sim, Thẻ cào
Sim, Thẻ cào
 Dịch vụ tiện ích
Dịch vụ tiện ích