Tứ phân vị là gì? 3 bước tính tứ phân vị Q1, Q2, Q3 cực dễ hiểu

Đóng góp bởi Dương Trúc Phương1 ngày trước

Tham khảo một số mẫu điện thoại giúp bạn học tập và tra cứu thông tin dễ dàng:

Trả chậm 0%

iPhone 17 Pro 256GB

Online giá rẻ quá

34.690.000₫

34.990.000₫

Trả chậm 0%

iPhone 17 Pro Max 256GB 37.990.000₫

Trả chậm 0% trả trước 0đ

Samsung Galaxy S25 FE 5G 8GB/256GB

15.490.000₫

18.490.000₫ -16%

Trả chậm 0% trả trước 0đ

Samsung Galaxy A17 5G 8GB/256GB

6.390.000₫

7.090.000₫ -9%

Trả chậm 0% trả trước 0đ

OPPO Find X9 Pro 5G 16GB/512GB 32.990.000₫

Trả chậm 0% trả trước 0đ

OPPO Find X9 5G 12GB/256GB 22.990.000₫

Trả chậm 0%

Xiaomi 15T Pro 5G 12GB/256GB 18.490.000₫

Trả chậm 0% trả trước 0đ

Xiaomi 15T 5G 12GB/256GB

13.490.000₫

13.990.000₫ -3%

Trả chậm 0% trả trước 0đ

vivo V60 Lite 5G 8GB/256GB 10.490.000₫

Xem thêm sản phẩm Điện thoại

Tứ phân vị là một trong những kiến thức thống kê cơ bản nhưng lại gây không ít bối rối cho nhiều người. Bài viết này sẽ giải thích rõ ràng tứ phân vị là gì, ý nghĩa của nó và hướng dẫn chi tiết các cách tính Q1, Q2, Q3 từ thủ công đến sử dụng công cụ một cách dễ hiểu nhất!

1. Tứ phân vị là gì?

Tứ phân vị (Quartile) là các giá trị thống kê chia một tập hợp dữ liệu đã sắp xếp thành bốn phần bằng nhau, mỗi phần chứa 25% số quan sát, giúp mô tả sự phân bố và mức độ phân tán của dữ liệu; bao gồm Tứ phân vị thứ nhất (Q1), thứ nhì (Q2 - Trung vị) và thứ ba (Q3).

Tứ phân vị thứ nhất (Q1): Còn gọi là phân vị thứ 25, là giá trị mà có 25% dữ liệu nhỏ hơn nó.
Tứ phân vị thứ hai (Q2): Còn gọi là phân vị thứ 50, đây chính là trung vị (Median) của toàn bộ tập dữ liệu, chia dãy số thành hai nửa bằng nhau.
Tứ phân vị thứ ba (Q3): Còn gọi là phân vị thứ 75, là giá trị mà có 75% dữ liệu nhỏ hơn nó.

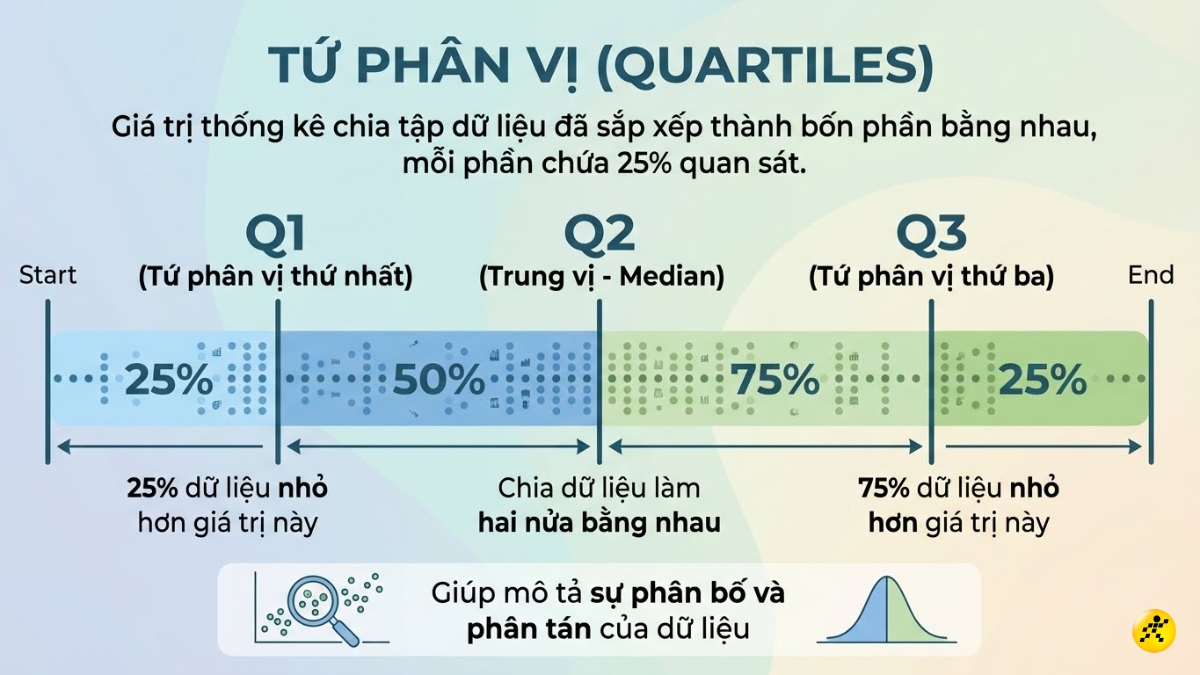
Tứ phân vị (Quartile)

2. Ý nghĩa của tứ phân vị và khoảng tứ phân vị (IQR)

Tứ phân vị không chỉ là những con số trong toán học, chúng cung cấp cái nhìn sâu sắc về cấu trúc và độ phân tán của dữ liệu, giúp việc phân tích dữ liệu trở nên hiệu quả hơn.

Đo lường độ phân tán: Tứ phân vị cho biết dữ liệu tập trung hay trải rộng ra sao mà không bị ành hưởng bởi các giá trị quá lớn hoặc quá nhỏ (giá trị ngoại lệ). Điều này khác biệt so với giá trị trung bình, vốn rất nhạy cảm với các giá trị này.
Cung cấp cái nhìn về cấu trúc dữ liệu: Giúp hiểu được sự phân bố của dữ liệu, ví dụ: 50% dữ liệu trung tâm nằm trong khoảng nào.
Nền tảng cho Biểu đồ hộp (Box Plot): Các giá trị tứ phân vị là cơ sở để vẽ biểu đồ hộp, một công cụ trực quan hóa dữ liệu rất mạnh mẽ.

Đặc biệt, khoảng tứ phân vị (Interquartile Range - IQR) là một khái niệm quan trọng khác. Nó được định nghĩa là hiệu số giữa tứ phân vị thứ ba và thứ nhất. Công thức tính như sau:

IQR = Q3 - Q1

Ý nghĩa của IQR là đại diện cho phạm vi của 50% dữ liệu nằm ở giữa, cho thấy mức độ biến động của phần trung tâm của tập dữ liệu. IQR càng lớn, dữ liệu càng phân tán.

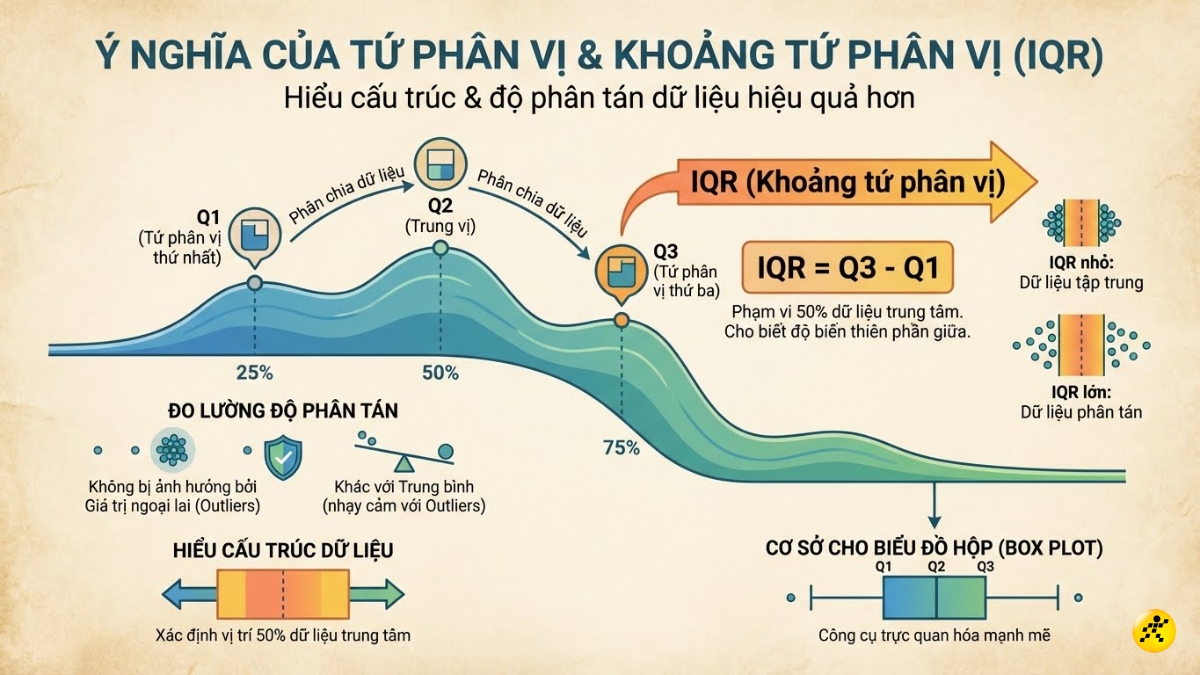
Ý nghĩa của tứ phân vị và khoảng tứ phân vị

3. Cách tính tứ phân vị thủ công (cho dữ liệu không ghép nhóm)

Để xác định các giá trị tứ phân vị cho một dãy số liệu rời rạc (dữ liệu không ghép nhóm), bạn cần tuân thủ quy trình 3 bước cơ bản sau đây.

Bước 1: Sắp xếp dữ liệu

Sắp xếp toàn bộ các giá trị trong mẫu số liệu theo thứ tự không giảm (từ nhỏ đến lớn). Đây là bước bắt buộc và quan trọng nhất.

Bước 2: Tìm tứ phân vị thứ hai (Q2 - Trung vị)

Xác định trung vị của cả dãy số. Nếu số phần tử n là lẻ, Q2 là số ở chính giữa. Nếu n là chẵn, Q2 là trung bình cộng của hai số ở giữa.

Bước 3: Tìm tứ phân vị thứ nhất (Q1) và thứ ba (Q3)

Chia dãy số thành hai nửa (nửa dưới và nửa trên) bởi Q2. Q1 là trung vị của nửa số liệu bên dưới (không bao gồm Q2 nếu n lẻ). Q3 là trung vị của nửa số liệu bên trên (không bao gồm Q2 nếu n lẻ).

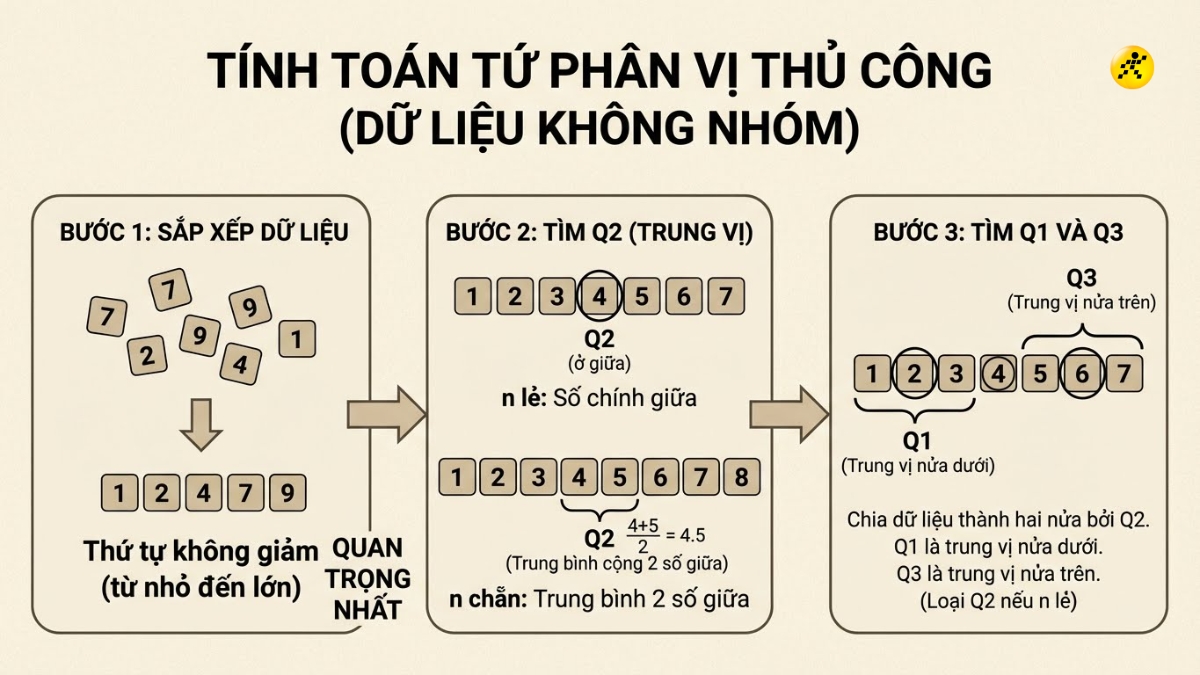
Cách tính tứ phân vị thủ công

Lưu ý quan trọng: Điểm khác biệt chính khi tính toán nằm ở Bước 2 và Bước 3, tùy thuộc vào số lượng dữ liệu (n) là số chẵn hay số lẻ. Hãy xem kỹ 2 ví dụ dưới đây để phân biệt rõ ràng.

4. Ví dụ minh họa tính tứ phân vị

Để hiểu rõ hơn, chúng ta sẽ cùng thực hành với hai bài tập tính tứ phân vị cụ thể cho hai trường hợp phổ biến nhất: số lượng dữ liệu là số lẻ và số chẵn.

Trường hợp 1: Dãy có số phần tử lẻ (n lẻ)

Bài toán: Tìm Q1, Q2, Q3 của dãy số: 3, 7, 8, 5, 12, 14, 21.

Bước	Thực hiện
1. Sắp xếp	Dãy số được sắp xếp lại: 3, 5, 7, 8, 12, 14, 21 (có n=7 phần tử).
2. Tìm Q2	Vì n=7 là số lẻ, Q2 là giá trị đứng ở vị trí chính giữa. Dãy số: 3, 5, 7, 8, 12, 14, 21. Vậy, Q2 = 8.
3. Tìm Q1, Q3	• Nửa dưới (không bao gồm Q2) là: 3, 5, 7. Trung vị của nửa này là 5. Vậy, Q1 = 5. • Nửa trên (không bao gồm Q2) là: 12, 14, 21. Trung vị của nửa này là 14. Vậy, Q3 = 14.
Kết luận	Q1 = 5, Q2 = 8, Q3 = 14.

Trường hợp 1: Dãy có số phần tử lẻ (n lẻ)

Trường hợp 2: Dãy có số phần tử chẵn (n chẵn)

Bài toán: Tìm Q1, Q2, Q3 của dãy số: 3, 6, 7, 10, 15, 18, 20, 22.

Bước	Thực hiện
1. Sắp xếp	Dãy số đã được sắp xếp (có n=8 phần tử).
2. Tìm Q2	Vì n=8 là số chẵn, Q2 là trung bình cộng của hai số ở giữa. Dãy số: 3, 6, 7, 10, 15, 18, 20, 22. Vậy, Q2 = (10 + 15) / 2 = 12.5.
3. Tìm Q1, Q3	• Nửa dưới là: 3, 6, 7, 10. Trung vị (Q1) là trung bình cộng của hai số giữa: (6 + 7) / 2 = 6.5. Vậy, Q1 = 6.5. • Nửa trên là: 15, 18, 20, 22. Trung vị (Q3) là trung bình cộng của hai số giữa: (18 + 20) / 2 = 19. Vậy, Q3 = 19.
Kết luận	Q1 = 6.5, Q2 = 12.5, Q3 = 19.

Trường hợp 2: Dãy có số phần tử chẵn (n chẵn)

5. Cách tính tứ phân vị bằng công cụ nhanh chóng

Ngoài cách tính thủ công, bạn hoàn toàn có thể sử dụng các công cụ quen thuộc như máy tính cầm tay hoặc phần mềm Excel để tìm tứ phân vị một cách nhanh chóng và chính xác.

Sử dụng máy tính Casio

Các dòng máy tính Casio phổ biến (như Casio fx-580VN X) đều có chức năng thống kê giúp bạn tìm tứ phân vị dễ dàng.

Bước 1: Mở chế độ Thống kê bằng cách nhấn MENU > chọn 6 (Statistics) > chọn 1 (1-Variable).

Bước 1: Mở chế độ Thống kê

Bước 2: Nhập toàn bộ dữ liệu của bạn vào cột x, sau mỗi giá trị nhấn phím =.

Nhập toàn bộ dữ liệu của bạn vào cột x

Bước 3: Sau khi nhập xong, nhấn phím OPTN, chọn 2 (1-Variable Calcs).

Nhấn phím OPTN, chọn 2

Bước 4: Màn hình sẽ hiển thị kết quả. Bạn chỉ cần kéo xuống để xem các giá trị Q1, med (chính là Q2) và Q3.

Màn hình sẽ hiển thị kết quả

Sử dụng hàm trong Microsoft Excel

Hàm QUARTILE.INC là công cụ mạnh mẽ trong Excel để tính toán tứ phân vị cho một vùng dữ liệu lớn, giúp bạn tiết kiệm thời gian đáng kể.

Cú pháp hàm: =QUARTILE.INC(array, quart)

array: Vùng dữ liệu bạn muốn tính tứ phân vị (ví dụ: A1:A10).
quart: Vị trí tứ phân vị bạn muốn tìm (Nhập 1 cho Q1, 2 cho Q2, 3 cho Q3).

Ví dụ: Để tìm Q1 của vùng dữ liệu từ ô A1 đến A10, bạn nhập công thức =QUARTILE.INC(A1:A10, 1).

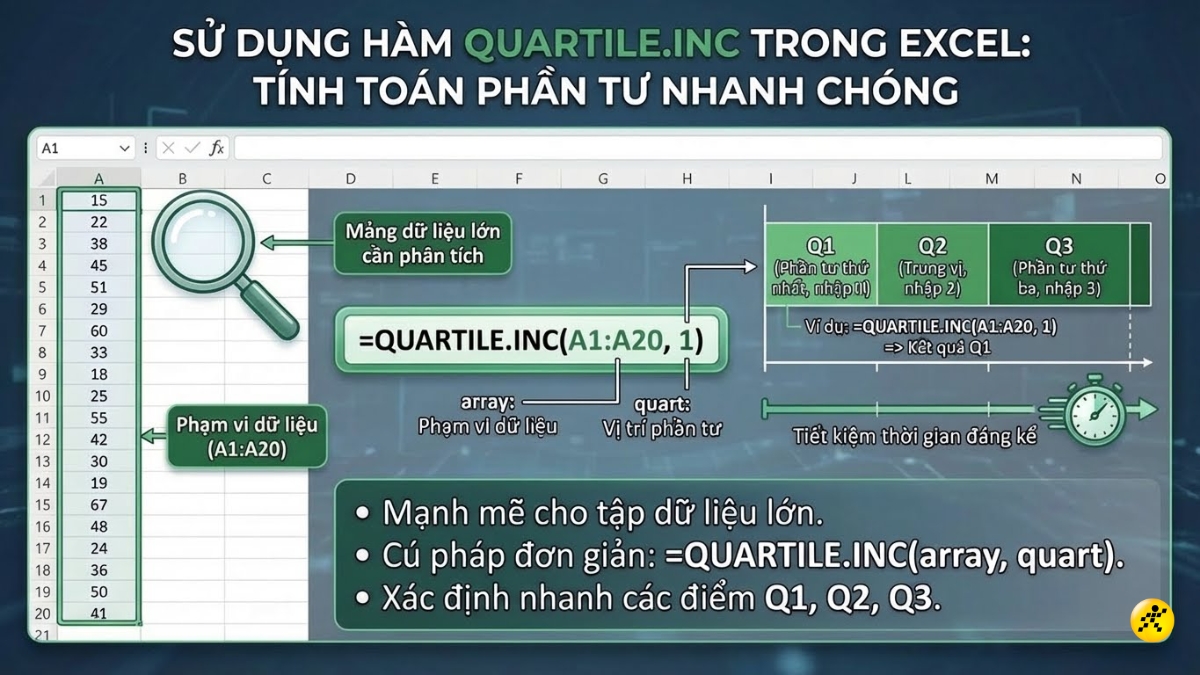
Sử dụng hàm trong Microsoft Excel

Xem thêm: Cách tính sin, cos, tan, cot trên máy tính cầm tay, máy tính bỏ túi

Tham khảo các mẫu laptop giá tốt để học tập và làm việc hiệu quả hơn:

Trả chậm 0%

MacBook Pro 14 inch M5 16GB/512GB 41.990.000₫

Trả chậm 0% trả trước 0đ

MacBook Air 13 inch M4 16GB/256GB

23.990.000₫

26.490.000₫ -9%

Trả chậm 0% trả trước 0đ

Dell 15 DC15250 i7 1355U (DC5I7748W1)

20.990.000₫

21.390.000₫

Trả chậm 0% trả trước 0đ

Lenovo IdeaPad Slim 3 15IRH10 i5 13420H (83K1000HVN)

15.890.000₫

16.990.000₫ -6%

Trả chậm 0% trả trước 0đ

Acer Aspire Lite 15 AL15 71P 517D i5 12450H (NX.J7KSV.001)

14.890.000₫

15.590.000₫

Trả chậm 0% trả trước 0đ

HP 15 fc0085AU R5 7430U (A6VV8PA)

14.590.000₫

15.790.000₫ -7%

Trả chậm 0% trả trước 0đ

Asus Vivobook Go 15 E1504FA R5 7520U (NJ776W)

13.590.000₫

14.190.000₫

Trả chậm 0%

MacBook Air 13 inch M2 16GB/256GB

19.690.000₫

24.490.000₫ -19%

Trả chậm 0% trả trước 0đ

Asus Gaming Vivobook 16X K3605VC i5 13420H (RP364W)

19.690.000₫

22.090.000₫ -10%

Xem thêm sản phẩm Laptop

6. Những lỗi sai thường gặp khi tính tứ phân vị

Việc tính toán tứ phân vị tuy có vẻ đơn giản nhưng người mới học rất dễ mắc phải những lỗi nhỏ dẫn đến kết quả sai lệch. Dưới đây là những lỗi phổ biến nhất cần tránh:

Không sắp xếp dữ liệu: Đây là lỗi sai cơ bản và nghiêm trọng nhất. Luôn phải sắp xếp dãy số từ nhỏ đến lớn trước khi thực hiện bất kỳ bước tính toán nào.
Xác định sai trung vị (Q2): Nhầm lẫn cách tính Q2 giữa trường hợp n chẵn và n lẻ là nguyên nhân phổ biến dẫn đến sai sốt.
Nhầm lẫn khi xác định nửa trên/dưới: Sai lầm thường gặp là gộp cả giá trị Q2 vào nửa dữ liệu dưới hoặc trên khi n là số lẻ, dẫn đến việc tính Q1 và Q3 bị sai.

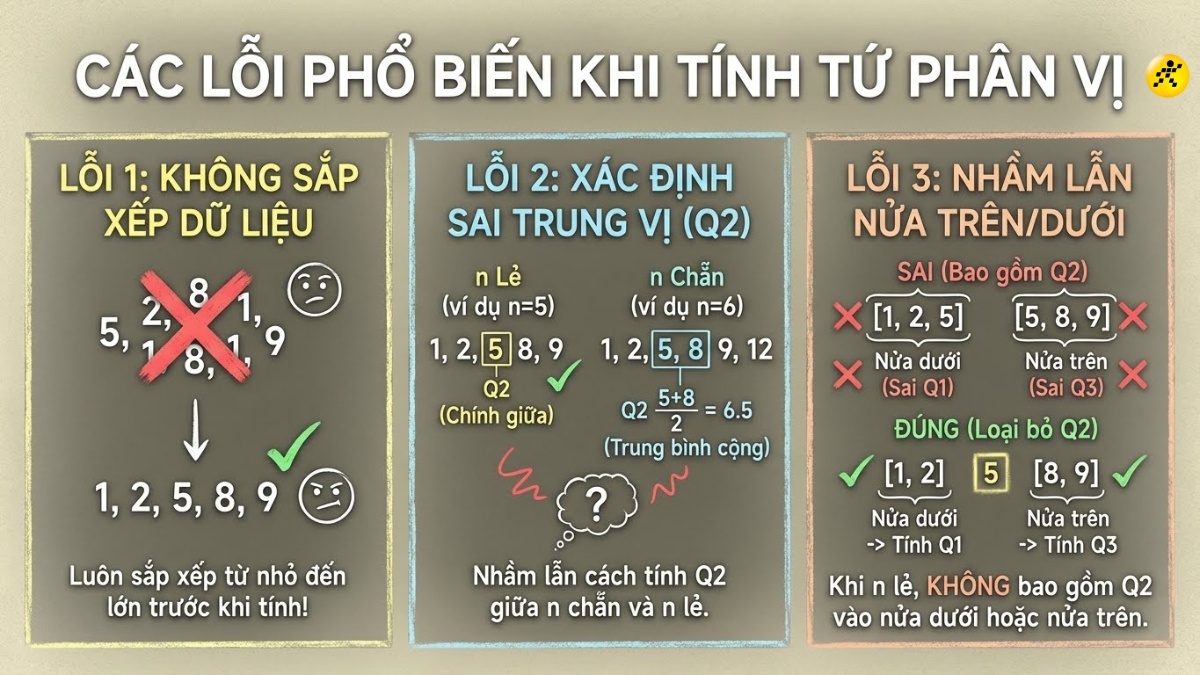
Những lỗi sai thường gặp khi tính tứ phân vị

7. Câu hỏi liên quan

Tứ phân vị và phân vị khác nhau như thế nào?

Tứ phân vị là các trường hợp đặc biệt của phân vị (Percentile). Cụ thể, Q1 là phân vị thứ 25, Q2 là phân vị thứ 50 và Q3 là phân vị thứ 75.

Tại sao không dùng giá trị trung bình mà lại dùng tứ phân vị?

Vì tứ phân vị và trung vị không bị ành hưởng bởi các giá trị quá lớn hoặc quá nhỏ (giá trị ngoại lệ), trong khi giá trị trung bình rất nhạy cảm với chúng. Điều này giúp tứ phân vị phản ánh độ phân tán của phần lớn dữ liệu một cách chính xác hơn.

Khoảng tứ phân vị (IQR) bằng 0 có ý nghĩa gì?

Điều này có nghĩa là 50% dữ liệu ở giữa của tập hợp không có sự biến động. Nói cách khác, ít nhất 50% giá trị trung tâm là giống hệt nhau, dẫn đến Q1, Q2 và Q3 có thể bằng nhau.

Cách tính tứ phân vị cho dữ liệu ghép nhóm có phức tạp không?

Có, cách tính cho dữ liệu ghép nhóm phức tạp hơn. Nó đòi hỏi sử dụng công thức nội suy dựa trên tần số và tần số tích lũy của các nhóm dữ liệu.

Có thể tính tứ phân vị trên điện thoại không?

Có, bạn có thể sử dụng các ứng dụng bảng tính như Google Sheets, Microsoft Excel trên điện thoại hoặc các ứng dụng máy tính khoa học để thực hiện các phép tính này.

Xem thêm các mẫu laptop đang kinh doanh tại Thế Giới Di Động:

Trả chậm 0%

MacBook Pro 14 inch M5 16GB/512GB 41.990.000₫

Trả chậm 0% trả trước 0đ

MacBook Air 13 inch M4 16GB/256GB

23.990.000₫

26.490.000₫ -9%

Trả chậm 0% trả trước 0đ

Dell 15 DC15250 i7 1355U (DC5I7748W1)

20.990.000₫

21.390.000₫

Trả chậm 0% trả trước 0đ

Lenovo IdeaPad Slim 3 15IRH10 i5 13420H (83K1000HVN)

15.890.000₫

16.990.000₫ -6%

Trả chậm 0% trả trước 0đ

Acer Aspire Lite 15 AL15 71P 517D i5 12450H (NX.J7KSV.001)

14.890.000₫

15.590.000₫

Trả chậm 0% trả trước 0đ

HP 15 fc0085AU R5 7430U (A6VV8PA)

14.590.000₫

15.790.000₫ -7%

Trả chậm 0% trả trước 0đ

Asus Vivobook Go 15 E1504FA R5 7520U (NJ776W)

13.590.000₫

14.190.000₫

Trả chậm 0%

MacBook Air 13 inch M2 16GB/256GB

19.690.000₫

24.490.000₫ -19%

Trả chậm 0% trả trước 0đ

Asus Gaming Vivobook 16X K3605VC i5 13420H (RP364W)

19.690.000₫

22.090.000₫ -10%

Xem thêm sản phẩm Laptop

Xem thêm:

Hy vọng bài viết đã giúp bạn hiểu rõ tứ phân vị là gì cũng như nắm vững các cách tính toán. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại để lại bình luận bên dưới nhé!

Từ khóa: cách tính tứ phân vị, tứ phân vị là gì, tứ phân vị là gì

Không tìm thấy kết quả phù hợp

Online giá rẻ quá

Đặt câu hỏi