Công thức tính chiều cao hình thang đầy đủ (ví dụ, bài tập, lời giải)

Đóng góp bởi Dương Trúc Phương14 giờ trước

Để tra cứu công thức và học tập hiệu quả, xem ngay các mẫu điện thoại mới nhất, GIÁ TỐT:

Trả chậm 0%

iPhone 17 Pro Max 256GB 37.990.000₫

Trả chậm 0% trả trước 0đ

OPPO Reno15 F 5G 12GB/256GB

12.490.000₫

12.990.000₫ -3%

Trả chậm 0%

iPhone 16 Pro Max 256GB

33.590.000₫

33.990.000₫ -1%

Trả chậm 0% trả trước 0đ

Samsung Galaxy A17 5G 8GB/256GB

6.390.000₫

7.090.000₫ -9%

Trả chậm 0% trả trước 0đ

Xiaomi Redmi Note 15 8GB/128GB 6.490.000₫

Trả chậm 0% trả trước 0đ

OPPO A6x 6GB/256GB 5.490.000₫

Trả chậm 0% trả trước 0đ

Xiaomi Redmi Note 15 Pro 5G 8GB/256GB 10.490.000₫

Trả chậm 0% trả trước 0đ

Samsung Galaxy A56 5G 8GB/256GB

9.890.000₫

10.790.000₫ -8%

Trả chậm 0% trả trước 0đ

Samsung Galaxy A06 5G 6GB/128GB

Online giá rẻ quá

3.150.000₫

4.110.000₫ -23%

Xem thêm sản phẩm Điện thoại

Việc tính chiều cao hình thang là một kiến thức cơ bản và quan trọng trong hình học, được ứng dụng trong nhiều bài toán từ đơn giản đến phức tạp. Xem ngay công thức tính chiều cao hình thang trong mọi trường hợp, kèm theo ví dụ và bài tập chi tiết!

1. Công thức tính chiều cao hình thang khi biết diện tích

Công thức này được suy ra trực tiếp từ công thức tính diện tích hình thang thông thường.

Công thức cụ thể: h = (2 x S) / (a + b)

Trong đó:

h: Là chiều cao của hình thang (đoạn thẳng vuông góc giữa hai đáy).
S: Là diện tích của hình thang.
a: Là độ dài cạnh đáy lớn.
b: Là độ dài cạnh đáy bé.

Công thức tính chiều cao hình thang khi biết diện tích

Lưu ý: Công thức này có thể áp dụng cho mọi loại hình thang, bao gồm hình thang thường, hình thang cân và hình thang vuông.

2. Ví dụ minh họa

Để giúp bạn hiểu rõ hơn cách vận dụng công thức, hãy cùng xét bài toán sau:

Cho một hình thang có diện tích S = 50 cm², đáy lớn a = 10 cm và đáy bé b = 5 cm. Yêu cầu tính chiều cao h của hình thang.

Bước 1: Xác định các đại lượng đã biết: S = 50, a = 10, b = 5.
Bước 2: Thay các giá trị vào công thức h = (2 x S) / (a + b).
Bước 3: Thực hiện phép tính: h = (2 x 50) / (10 + 5) = 100 / 15.
Bước 4: Kết luận chiều cao hình thang xấp xỉ 6.67 cm.

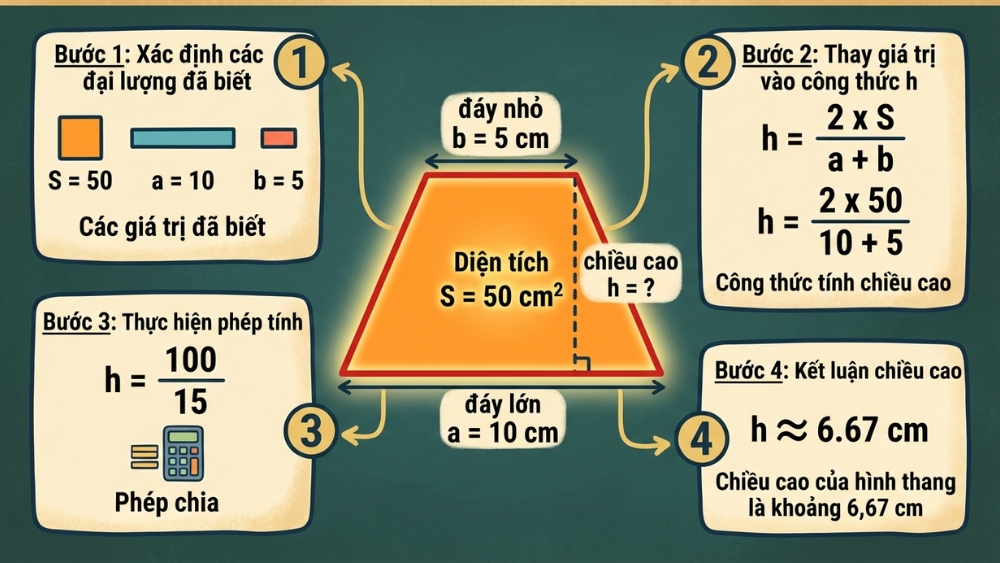
Ví dụ minh họa

Lưu ý quan trọng: Khi áp dụng công thức, bạn cần đảm bảo rằng tất cả các đơn vị đo (diện tích, độ dài đáy) phải đồng nhất. Nếu diện tích là cm² thì độ dài các cạnh đáy cũng phải là cm.

Sắm ngay laptop cấu hình tốt để học tập và tra cứu công thức dễ dàng:

Trả chậm 0% trả trước 0đ

MacBook Air 13 inch M4 16GB/256GB

23.990.000₫

26.490.000₫ -9%

Trả chậm 0% trả trước 0đ

HP 15 fc0655AU R5 7430U (C81NGPA)

14.990.000₫

15.790.000₫ -5%

Trả chậm 0% trả trước 0đ

Asus Vivobook Go E1504FA R5 7520U (BQ1160W)

Online giá rẻ quá

14.490.000₫

14.990.000₫

Trả chậm 0%

MacBook Air 13 inch M2 16GB/256GB

19.690.000₫

24.490.000₫ -19%

Trả chậm 0% trả trước 0đ

Dell 15 DC15250 i5 1334U (DC5I5357W1)

17.490.000₫

19.390.000₫ -9%

Trả chậm 0% trả trước 0đ

Lenovo IdeaPad Slim 3 15IRH10 i5 13420H (83K1000HVN)

16.690.000₫

18.990.000₫ -12%

Trả chậm 0% trả trước 0đ

HP 245 G10 R5 7530U (B8PF9AT)

13.490.000₫

14.290.000₫ -5%

Trả chậm 0% trả trước 0đ

Asus Vivobook 15 X1504VA Core 5 120U (BQ185WS)

17.490.000₫

19.190.000₫ -8%

Trả chậm 0% trả trước 0đ

Asus Vivobook 15 X1504VA i3 1315U (BQ3394W)

12.790.000₫

13.990.000₫ -8%

Xem thêm sản phẩm Laptop

3. Cách tính chiều cao hình thang trong trường hợp đặc biệt

Trong một số trường hợp đặc biệt như hình thang vuông hoặc hình thang cân, chúng ta có thể tính chiều cao mà không cần biết trước diện tích, thay vào đó sẽ dựa vào các yếu tố khác như cạnh bên hoặc góc.

Đối với hình thang vuông

Hình thang vuông là trường hợp đơn giản nhất vì một cạnh bên của nó đã vuông góc sẵn với hai đáy. Trong trường hợp này, chiều cao của hình thang vuông chính là độ dài của cạnh bên vuông góc đó. Bạn không cần thực hiện các phép tính toán phức tạp.

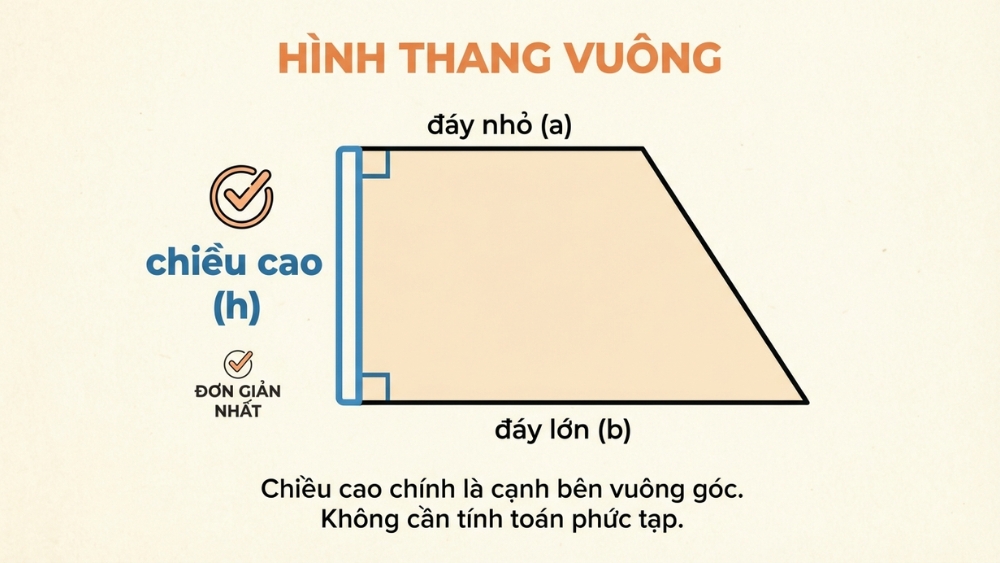
Chiều cao của hình thang vuông là độ dài của cạnh bên vuông góc

Đối với hình thang cân (khi biết cạnh bên và hai đáy)

Bạn có thể sử dụng định lý Pythagoras để tìm chiều cao hình thang cân khi đã biết độ dài các cạnh. Cách thực hiện như sau:

Bước 1: Từ một đỉnh ở đáy bé, hạ một đường cao xuống đáy lớn. Đường cao này sẽ tạo ra một tam giác vuông.
Bước 2: Xác định cạnh huyền của tam giác vuông chính là cạnh bên (c) của hình thang. Cạnh đáy của tam giác này (x) được tính bằng: x = (a - b) / 2.
Bước 3: Áp dụng định lý Pythagoras: c² = h² + x².
Bước 4: Suy ra công thức tính chiều cao: h = √(c² - ((a - b) / 2)²).

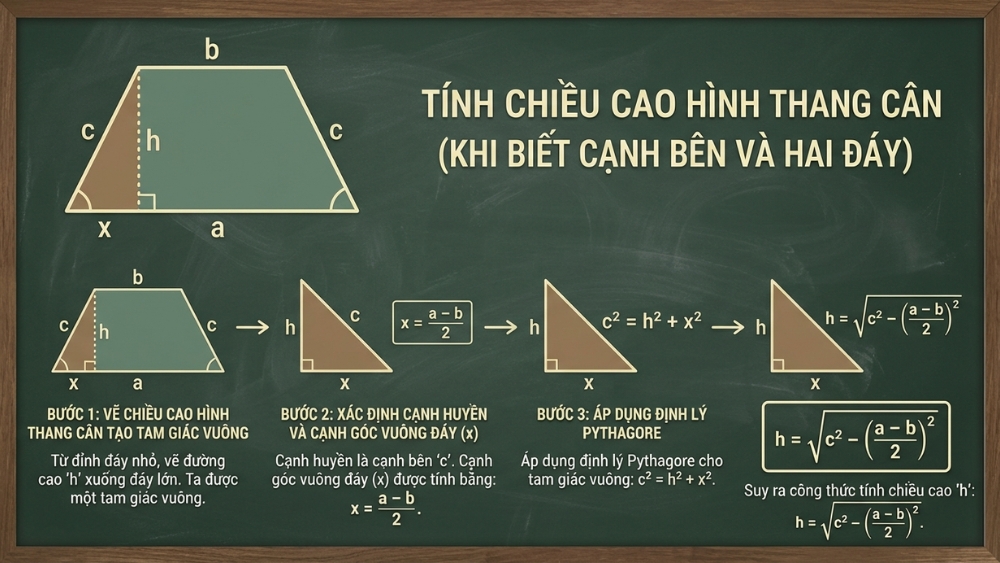
Cách tính chiều cao hình thang cân

4. Bảng so sánh nhanh các cách tính chiều cao hình thang

Trường hợp	Dữ kiện cần biết	Công thức tính chiều cao (h)
Hình thang bất kỳ	Diện tích (S), đáy lớn (a), đáy bé (b)	h = (2 x S) / (a + b)
Hình thang vuông	Độ dài cạnh bên vuông góc (c)	h = c
Hình thang cân	Đáy lớn (a), đáy bé (b), cạnh bên (c)	h = √(c² - ((a-b)/2)²)

5. Câu hỏi liên quan

Chiều cao hình thang có phải luôn là cạnh bên không?

Không, chiều cao hình thang chỉ là cạnh bên trong trường hợp đặc biệt duy nhất là hình thang vuông. Đối với các loại hình thang khác, chiều cao là đường thẳng hạ vuông góc từ một đáy xuống đáy còn lại.

Làm thế nào để tính diện tích hình thang khi biết chiều cao?

Khi đã có chiều cao, bạn có thể tính diện tích hình thang bằng công thức: S = (a + b) x h / 2 (tổng đáy nhân chiều cao rồi chia đôi).

Đơn vị của chiều cao là gì?

Đơn vị của chiều cao là đơn vị đo độ dài thông thường (như cm, m, mm...) và phải đồng nhất với đơn vị của các cạnh đáy trong cùng một phép tính.

Đường trung bình của hình thang là gì?

Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên. Độ dài đường trung bình bằng nửa tổng hai đáy: m = (a + b) / 2.

Xem thêm các mẫu điện thoại khác đang kinh doanh tại Thế Giới Di Động:

Trả chậm 0%

iPhone 17 Pro Max 256GB 37.990.000₫

Trả chậm 0% trả trước 0đ

OPPO Reno15 F 5G 12GB/256GB

12.490.000₫

12.990.000₫ -3%

Trả chậm 0%

iPhone 16 Pro Max 256GB

33.590.000₫

33.990.000₫ -1%

Trả chậm 0% trả trước 0đ

Samsung Galaxy A17 5G 8GB/256GB

6.390.000₫

7.090.000₫ -9%

Trả chậm 0% trả trước 0đ

Xiaomi Redmi Note 15 8GB/128GB 6.490.000₫

Trả chậm 0% trả trước 0đ

OPPO A6x 6GB/256GB 5.490.000₫

Trả chậm 0% trả trước 0đ

Xiaomi Redmi Note 15 Pro 5G 8GB/256GB 10.490.000₫

Trả chậm 0% trả trước 0đ

Samsung Galaxy A56 5G 8GB/256GB

9.890.000₫

10.790.000₫ -8%

Trả chậm 0% trả trước 0đ

Samsung Galaxy A06 5G 6GB/128GB

Online giá rẻ quá

3.150.000₫

4.110.000₫ -23%

Xem thêm sản phẩm Điện thoại

Xem thêm:

Trên đây là tổng hợp đầy đủ các công thức tính chiều cao hình thang từ trường hợp tổng quát đến các dạng đặc biệt. Hy vọng bài viết sẽ giúp bạn nắm vững kiến thức và áp dụng thành công vào việc giải các bài toán hình học trong tương lai.

Không tìm thấy kết quả phù hợp

Đặt câu hỏi