Tham khảo một số mẫu laptop cấu hình tốt, hỗ trợ học tập và làm việc hiệu quả:
Hình thoi là kiến thức hình học quan trọng từ tiểu học đến trung học. Việc nắm vững các công thức tính diện tích hình thoi giúp bạn giải quyết bài tập chính xác và nhanh chóng. Khám phá ngay 3 cách tính diện tích hình thoi hiệu quả nhất!
1. Hình thoi là hình gì?
Hình thoi là một tứ giác đặc biệt có bốn cạnh bằng nhau, hai đường chéo vuông góc với nhau tại trung điểm mỗi đường, đồng thời là đường phân giác của các góc. Có các góc đối bằng nhau và là một dạng của hình bình hành có hai cạnh kề bằng nhau.
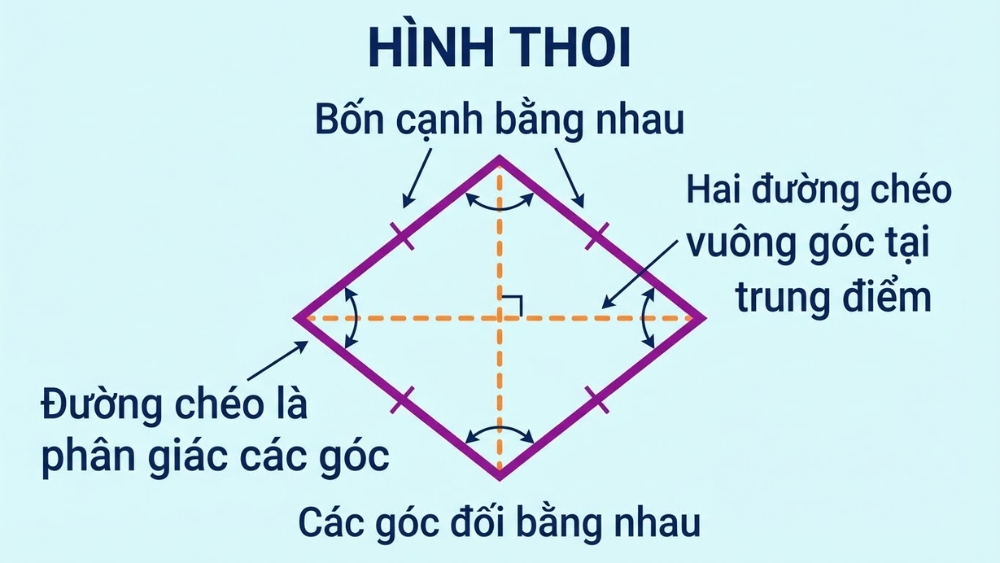
Hình thoi là một tứ giác đặc biệt
2. Tổng hợp các công thức tính diện tích hình thoi
Tùy vào dữ kiện mà bài toán cung cấp như độ dài đường chéo, cạnh đáy, chiều cao hay số đo góc, chúng ta sẽ áp dụng các phương pháp tính toán khác nhau.
Tính diện tích hình thoi dựa vào độ dài hai đường chéo
Đây là công thức phổ biến nhất, thường được giảng dạy trong chương trình Toán lớp 4. Phương pháp này áp dụng khi bạn đã biết độ dài của hai đường chéo đi qua tâm hình thoi.
Công thức: S = (d1 * d2) / 2
Giải thích các đại lượng:
- S: Diện tích của hình thoi.
- d₁: Độ dài đường chéo thứ nhất.
- d₂: Độ dài đường chéo thứ hai.
Ví dụ minh họa: Tính diện tích hình thoi ABCD biết độ dài hai đường chéo lần lượt là AC = 12 cm và BD = 10 cm.
S = (12 * 10) / 2 = 60 (cm²).
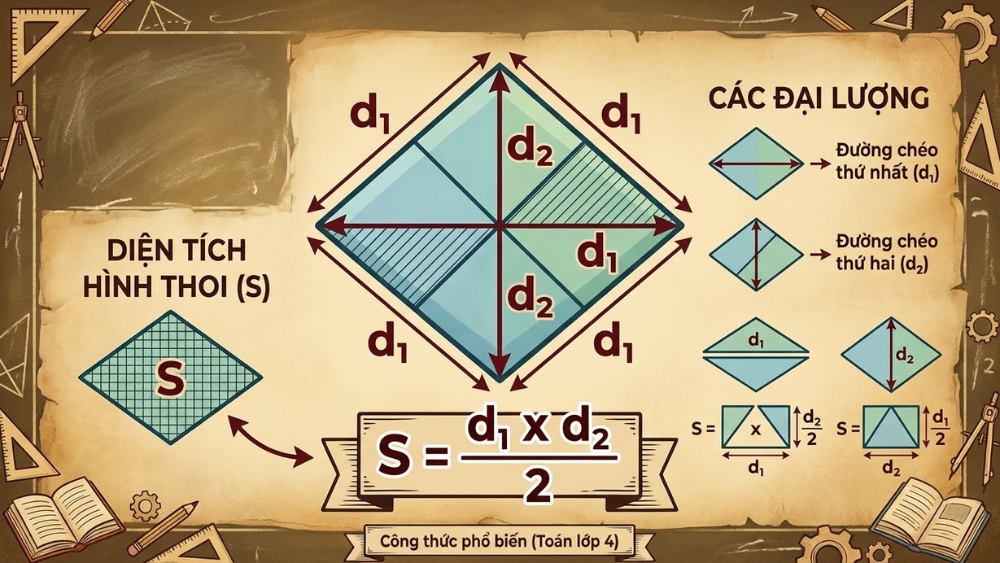
Tính diện tích hình thoi dựa vào độ dài hai đường chéo
Tính diện tích hình thoi dựa vào cạnh đáy và chiều cao
Vì hình thoi bản chất là một hình bình hành, nên nếu bài toán cung cấp độ dài một cạnh và chiều cao tương ứng, bạn có thể áp dụng công thức tính diện tích hình bình hành.
Công thức: S = a * h
Giải thích các đại lượng:
- a: Độ dài một cạnh của hình thoi (cạnh đáy).
- h: Chiều cao của hình thoi (khoảng cách vuông góc từ một đỉnh đến cạnh đối diện).
Ví dụ minh họa: Cho hình thoi có độ dài cạnh là 8 cm và chiều cao hạ từ đỉnh xuống cạnh đối diện là 5 cm. Tính diện tích.
S = 8 * 5 = 40 (cm²).
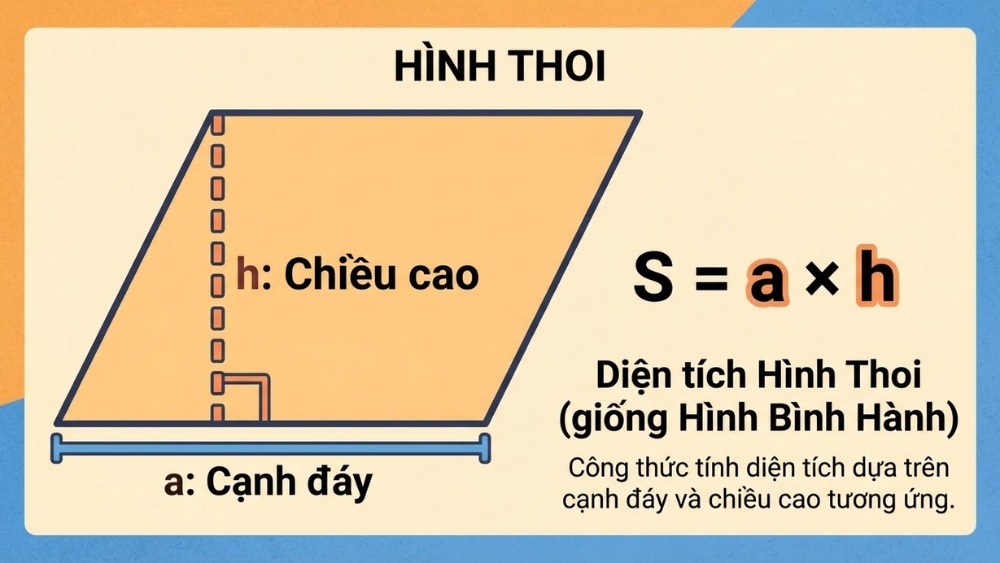
Tính diện tích hình thoi dựa vào cạnh đáy và chiều cao
Tính diện tích hình thoi bằng công thức lượng giác (Nâng cao)
Công thức này thường được áp dụng cho học sinh cấp trung học cơ sở hoặc trung học phổ thông khi bài toán cho biết độ dài cạnh và số đo của một góc trong hình thoi.
Công thức: S = a² * sin(α)
Giải thích các đại lượng:
- a: Độ dài cạnh của hình thoi.
- α: Số đo của một góc bất kỳ trong hình thoi (thường là góc nhọn giữa hai cạnh kề).
- sin: Hàm lượng giác của góc α.
Ví dụ minh họa: Tính diện tích hình thoi có cạnh dài 6 cm và một góc trong hình bằng 30°.
S = 6² * sin(30°) = 36 * 0.5 = 18 (cm²).
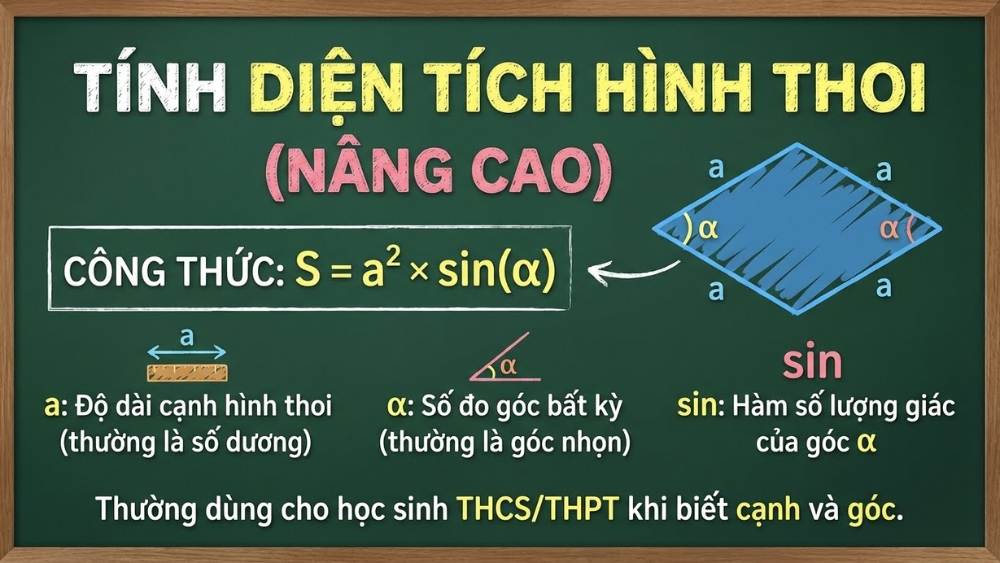
Tính diện tích hình thoi bằng công thức lượng giác
Bạn cũng có thể dễ dàng giải các bài toán hình học trên các mẫu máy tính bảng:
3. Bảng so sánh các phương pháp tính diện tích hình thoi
Bảng dưới đây tóm tắt các trường hợp sử dụng để bạn dễ dàng lựa chọn công thức phù hợp với đề bài:
|
Phương pháp tính
|
Công thức
|
Dữ kiện cần có
|
Phân khúc áp dụng
|
|
Qua đường chéo
|
S = (d1 * d2) / 2
|
Độ dài 2 đường chéo
|
Cơ bản (Tiểu học & THCS)
|
|
Qua cạnh và chiều cao
|
S = a * h
|
Độ dài cạnh và chiều cao
|
Cơ bản (THCS)
|
|
Qua lượng giác
|
S = a² * sin(α)
|
Độ dài cạnh và số đo góc
|
Nâng cao (THCS & THPT)
|
4. Các dạng bài tập vận dụng chi tiết
Để ghi nhớ lâu hơn, bạn nên thực hành qua các dạng toán từ cơ bản đến thực tế.
Dạng 1: Bài toán thuận cơ bản
Đề bài: Tính diện tích một miếng bìa hình thoi có hai đường chéo dài lần lượt là 20 cm và 34 cm.
Lời giải:
Diện tích miếng bìa hình thoi là: S = (20 * 34) / 2 = 340 (cm²)
Đáp số: 340 cm².
Dạng 2: Tìm độ dài đường chéo khi biết diện tích
Đề bài: Một hình thoi có diện tích là 100 cm², biết độ dài một đường chéo là 10 cm. Tính độ dài đường chéo còn lại.
Lời giải:
Độ dài đường chéo còn lại của hình thoi là:
d2 = (S * 2) / d1 = (100 * 2) / 10 = 20 (cm)
Đáp số: 20 cm.
Dạng 3: Bài toán ứng dụng thực tế
Đề bài: Một viên gạch men hình thoi có độ dài hai đường chéo là 30 cm và 40 cm. Tính diện tích của 50 viên gạch như thế.
Lời giải:
Diện tích của một viên gạch hình thoi là: (30 * 40) / 2 = 600 (cm²)
Diện tích của 50 viên gạch men là: 600 * 50 = 30.000 (cm²) = 3 (m²)
Đáp số: 3 m².
Dạng 4: Kết hợp cạnh và chiều cao
Đề bài: Hình thoi có cạnh dài 15 cm và chiều cao tương ứng là 7 cm. Tính diện tích và số lượng hình thoi cần để lát 10 m² sàn nhà (giả sử không hao hụt).
Lời giải:
Diện tích một hình thoi: S = 15 * 7 = 105 (cm²) = 0.0105 (m²)
Số lượng cần: 10 / 0.0105 ≈ 952 hình thoi
Đáp số: Diện tích 0.0105 m²; cần khoảng 952 hình.
Dạng 5: Lượng giác ứng dụng
Đề bài: Hình thoi có cạnh 10 cm và góc nhọn 60°. Tính diện tích, sau đó tìm đường chéo lớn nếu đường chéo nhỏ là 12 cm.
Lời giải:
Diện tích: S = 10^2 * sin(60°) = 100 * 0.866 ≈ 86.6 (cm²)
Đường chéo lớn: d2 = (S * 2) / 12 ≈ (86.6 * 2) / 12 ≈ 14.4 (cm)
Đáp số: Diện tích ≈ 86.6 cm²; d2 ≈ 14.4 cm.
5. Cách tính chu vi hình thoi
Chu vi của hình thoi là tổng độ dài của bốn cạnh xung quanh hình đó. Vì bốn cạnh của hình thoi bằng nhau, công thức tính chu vi rất tương đồng với hình vuông.
Công thức: P = a * 4
Trong đó:
- P: Chu vi hình thoi.
- a: Độ dài của một cạnh.
Ví dụ: Một hình thoi có cạnh dài 15 cm. Chu vi của hình thoi đó là:
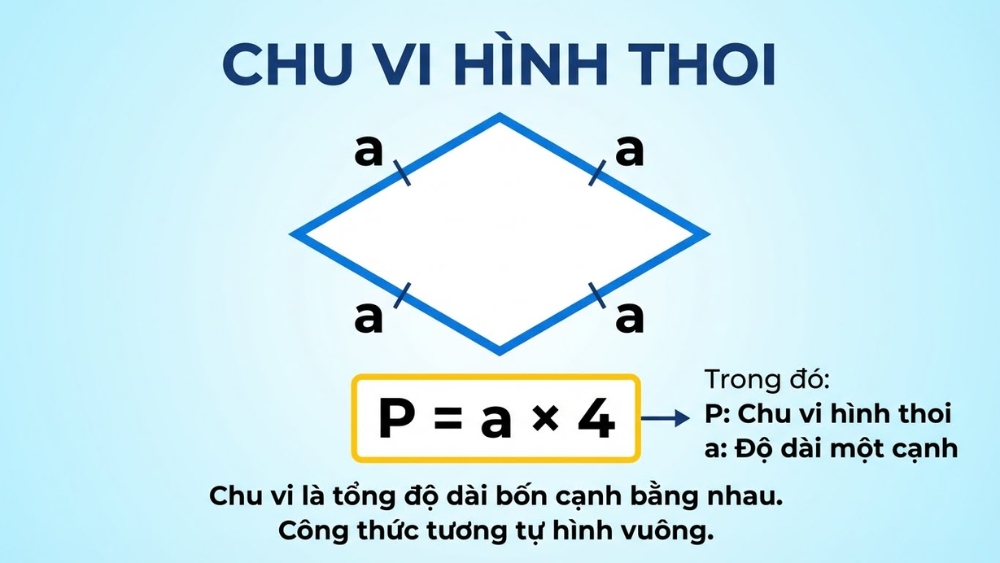
Cách tính chu vi hình thoi
6. Những câu hỏi thường gặp
Hình vuông có phải là một hình thoi không?
Có. Hình vuông là một trường hợp đặc biệt của hình thoi vì nó có đầy đủ các tính chất của hình thoi (4 cạnh bằng nhau, đường chéo vuông góc). Ngoài ra, hình vuông còn có thêm tính chất là 4 góc vuông và 2 đường chéo bằng nhau.
Tại sao diện tích hình thoi lại bằng nửa tích hai đường chéo?
Giải thích theo hình học: Khi bạn vẽ hai đường chéo, hình thoi sẽ được chia thành 4 tam giác vuông bằng nhau. Tổng diện tích của 4 tam giác này chính bằng diện tích hình thoi, dẫn đến công thức (d1 * d2) / 2.
Đơn vị đo diện tích hình thoi cần lưu ý điều gì?
Khi thực hiện tính toán, bạn phải đảm bảo các thông số đầu vào (cạnh, đường chéo) có cùng đơn vị đo (ví dụ cùng là cm hoặc cùng là m). Kết quả diện tích luôn mang đơn vị vuông (cm², m²,...).
Sắm ngay các mẫu laptop học tập - văn phòng giá tốt, chính hãng:
Cảm ơn bạn đã theo dõi bài viết. Việc hiểu rõ bản chất và áp dụng linh hoạt 3 công thức tính diện tích hình thoi trên sẽ giúp kết quả học tập của bạn được cải thiện rõ rệt. Chúc bạn vận dụng thành công vào các bài kiểm tra sắp tới!
 Điện thoại
Điện thoại
 Laptop
Laptop
 Phụ kiện
Phụ kiện
 Smartwatch
Smartwatch
 Đồng hồ
Đồng hồ
 Tablet
Tablet
 Máy cũ, Thu cũ
Máy cũ, Thu cũ
 Màn hình, Máy in
Màn hình, Máy in
 Sim, Thẻ cào
Sim, Thẻ cào
 Dịch vụ tiện ích
Dịch vụ tiện ích