Công thức tính diện tích hình tam giác (vuông, đều, cân) dễ nhớ

Đóng góp bởi Dương Trúc Phương2 ngày trước

Bạn có thể dễ dàng tính toán các công thức này trên các mẫu điện thoại đang kinh doanh tại TGDĐ:

Trả chậm 0%

iPhone 17 Pro 256GB

Online giá rẻ quá

34.690.000₫

34.990.000₫

Trả chậm 0%

iPhone 17 Pro Max 256GB 37.990.000₫

Trả chậm 0% trả trước 0đ

Samsung Galaxy S25 FE 5G 8GB/256GB

15.490.000₫

18.490.000₫ -16%

Trả chậm 0% trả trước 0đ

Samsung Galaxy A17 5G 8GB/256GB

6.390.000₫

7.090.000₫ -9%

Trả chậm 0% trả trước 0đ

OPPO Find X9 Pro 5G 16GB/512GB 32.990.000₫

Trả chậm 0% trả trước 0đ

OPPO Find X9 5G 12GB/256GB 22.990.000₫

Trả chậm 0%

Xiaomi 15T Pro 5G 12GB/256GB 18.490.000₫

Trả chậm 0% trả trước 0đ

Xiaomi 15T 5G 12GB/256GB

13.490.000₫

13.990.000₫ -3%

Trả chậm 0% trả trước 0đ

vivo V60 Lite 5G 8GB/256GB 10.490.000₫

Xem thêm sản phẩm Điện thoại

Hình tam giác là một trong những hình học cơ bản và quen thuộc nhất. Tuy nhiên, không phải ai cũng nhớ hết các công thức tính diện tích của nó. Bài viết này sẽ tổng hợp đầy đủ các công thức tính diện tích hình tam giác cho mọi trường hợp, giúp bạn giải quyết bài toán một cách nhanh chóng và chính xác nhất!

1. Các công thức tính diện tích hình tam giác nhanh nhất

Để giải quyết bài toán tính diện tích tam giác, bạn cần chọn đúng công thức dựa trên các dữ kiện đã biết như chiều cao, độ dài các cạnh, hay số đo góc. Dưới đây là bảng tổng hợp nhanh các công thức phổ biến nhất giúp bạn dễ dàng tra cứu.

Các công thức tính diện tích hình tam giác

Thông tin biết	Loại tam giác	Công thức cần dùng
Độ dài cạnh đáy và chiều cao tương ứng	Mọi loại tam giác	S = 1/2 × a × h
Độ dài hai cạnh góc vuông	Tam giác vuông	S = 1/2 × a × b
Độ dài 3 cạnh	Mọi loại tam giác	Công thức Heron: S = √[p(p − a)(p − b)(p − c)] với p = (a + b + c) / 2
Độ dài 2 cạnh và góc xen giữa	Mọi loại tam giác	S = 1/2 × a × b × sin(C)
Độ dài 1 cạnh	Tam giác đều	S = (a²√3) / 4

2. Tính diện tích tam giác bằng chiều cao và cạnh đáy (cơ bản)

Đây là công thức phổ biến và được dạy từ bậc tiểu học, áp dụng được cho mọi loại tam giác từ thường, cân, đều cho đến tam giác vuông. Quy tắc "lấy đáy nhân cao chia 2" chính là nền tảng của hình học Euclid.

Công thức: S = 1/2 × a × h

Trong đó:

S: là diện tích tam giác.
a: là độ dài cạnh đáy.
h: là chiều cao, được hạ từ đỉnh đối diện vuông góc với cạnh đáy a.

Ví dụ: Cho tam giác ABC có cạnh đáy BC = 10 cm và chiều cao tương ứng AH = 6 cm. Diện tích tam giác ABC được tính như sau: S = 1/2 x 10 x 6 = 30 cm².

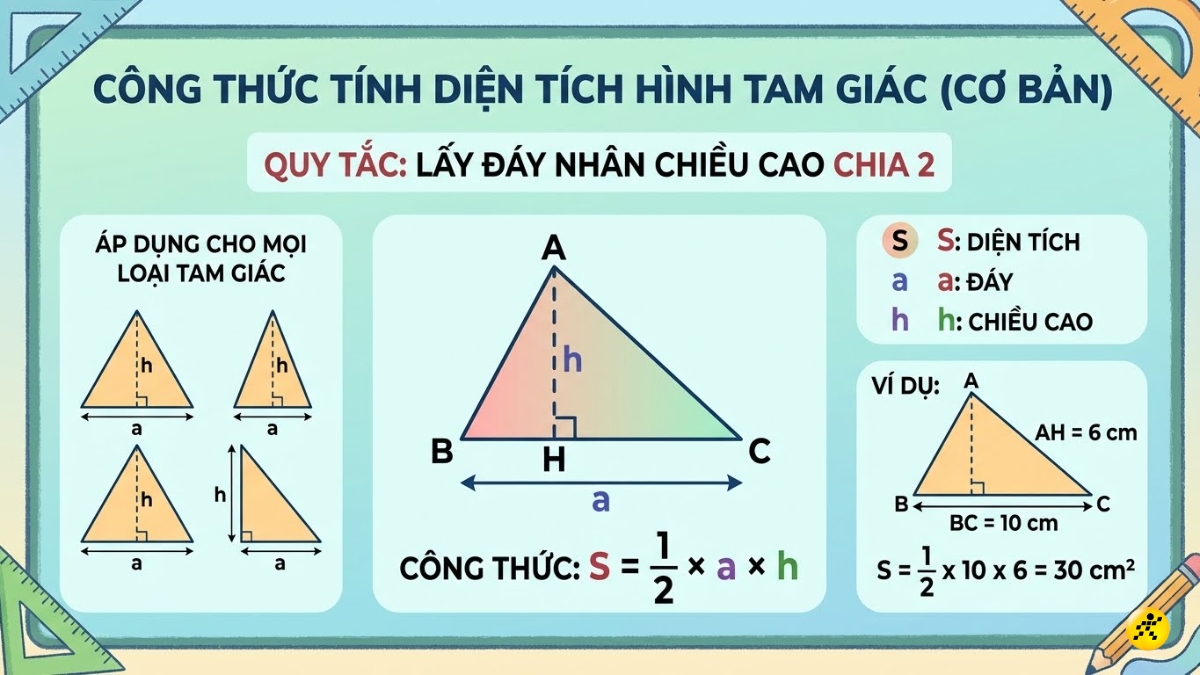
Tính diện tích tam giác bằng chiều cao và cạnh đáy

3. Công thức Heron (khi biết độ dài 3 cạnh)

Khi bài toán không cho chiều cao nhưng lại cung cấp đủ độ dài 3 cạnh, công thức Heron (được đặt theo tên nhà toán học Heron của Alexandria) là công cụ mạnh mẽ nhất để bạn sử dụng. Đây là cách giải quyết hiệu quả khi không có dữ kiện về góc hay đường cao.

Bước 1: Tính nửa chu vi của tam giác (p). Nửa chu vi là tổng độ dài 3 cạnh chia cho 2.

Công thức: p = (a+b+c)/2

Bước 2: Áp dụng công thức Heron.

Công thức: S = p x (p - a) x (p - b) x (p - c)

Ví dụ: Một tam giác có 3 cạnh lần lượt là 5 cm, 6 cm, 7 cm.

Tính nửa chu vi: p = (5 + 6 + 7) / 2 = 9 cm.
Áp dụng công thức Heron: S = √[9 * (9-5) * (9-6) * (9-7)] = √[9 * 4 * 3 * 2] = √216 ≈ 14.7 cm².

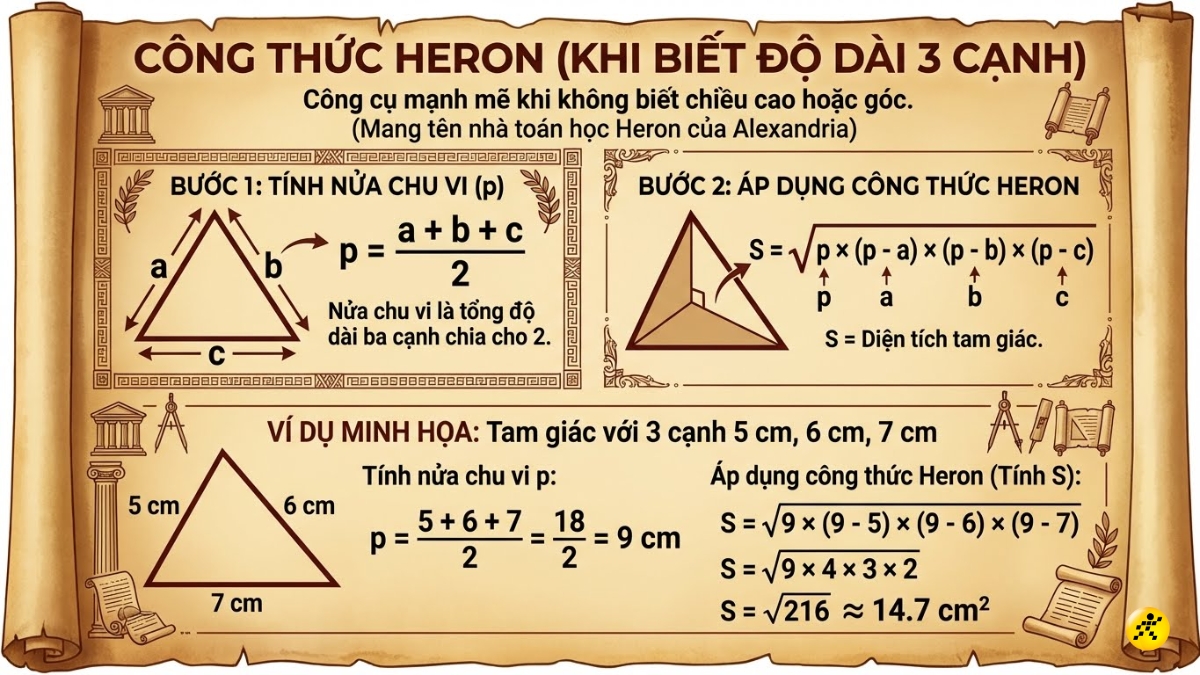
Công thức Heron

4. Công thức lượng giác (khi biết 2 cạnh và góc xen giữa)

Trong lượng giác, bạn có thể dễ dàng tìm ra diện tích của một tam giác nếu biết độ dài hai cạnh và số đo của góc được tạo bởi chính hai cạnh đó. Phương pháp này dựa trên định lý sin trong tam giác.

Công thức: Diện tích tam giác bằng một nửa tích của hai cạnh nhân với sin của góc xen giữa chúng.

S = 1/2 x a x b x sin(C)

S = 1/2 x b x c x sin(A)

S = 1/2 x a x c x sin(B)

Ví dụ: Tam giác ABC có cạnh a = 8 cm, cạnh b = 10 cm và góc C = 30 độ.

Áp dụng công thức: S = 1/2 * 8 * 10 * sin(30°) = 1/2 * 80 * 0.5 = 20 cm². Để tính toán nhanh, bạn có thể sử dụng ứng dụng máy tính khoa học trên điện thoại.

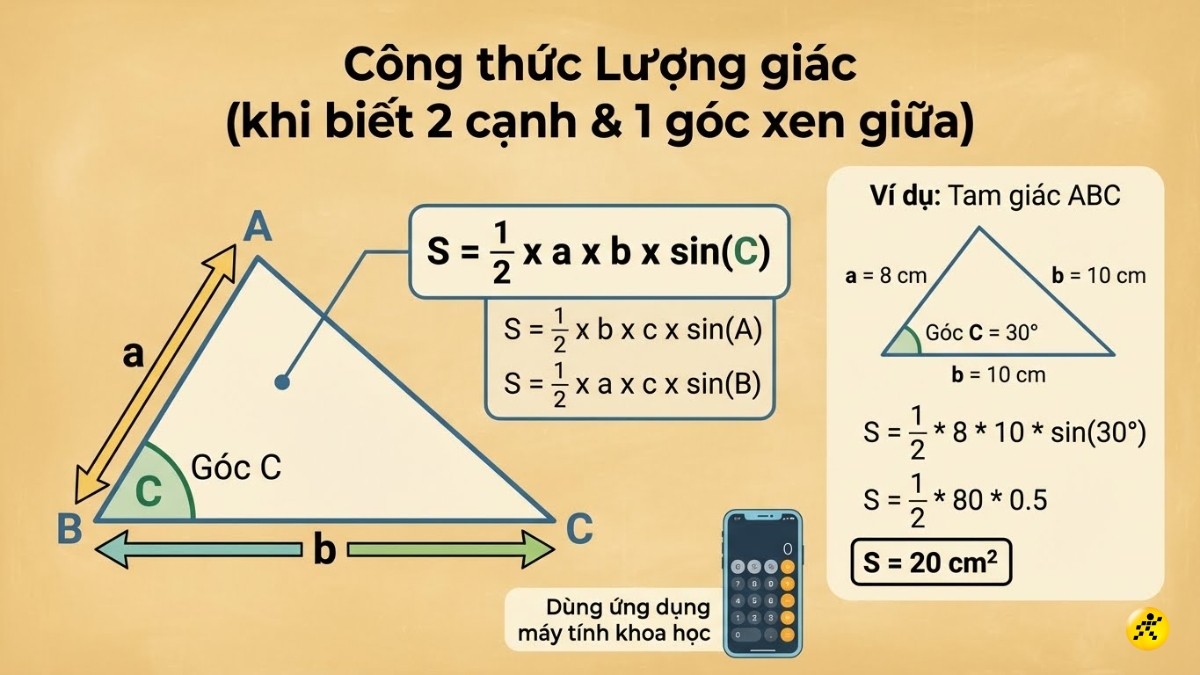
Công thức lượng giác

Xem thêm: Cách tính sin, cos, tan, cot trên máy tính cầm tay, máy tính bỏ túi

5. Công thức cho các tam giác đặc biệt

Đối với các tam giác có tính chất đặc biệt như tam giác vuông, cân hoặc đều, chúng ta có những công thức tính nhanh giúp tiết kiệm thời gian hơn so với việc áp dụng công thức cơ bản.

Tam giác vuông

Trong tam giác vuông, hai cạnh góc vuông đóng vai trò vừa là cạnh, vừa là đường cao của nhau. Vì vậy, công thức cơ bản được đơn giản hóa đi rất nhiều.

Công thức: S = 1/2 × a × b

(với a, b là độ dài 2 cạnh góc vuông)

Diện tích tam giác vuông bằng một nửa tích độ dài hai cạnh góc vuông

Ví dụ: Tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm. Diện tích là: S = 1/2 * 6 * 8 = 24 cm².

Công thức tam giác vuông

Tam giác đều

Tam giác đều là tam giác có cả ba cạnh bằng nhau và ba góc bằng 60 độ. Từ đặc điểm này, ta có một công thức tính nhanh rất tiện lợi.

Công thức: S = (a^2 x √3 )/ 4

(với a là độ dài cạnh của tam giác).

Ví dụ: Tam giác đều có cạnh 4 cm. Diện tích là: S = (4² * √3) / 4 = 4√3 cm².

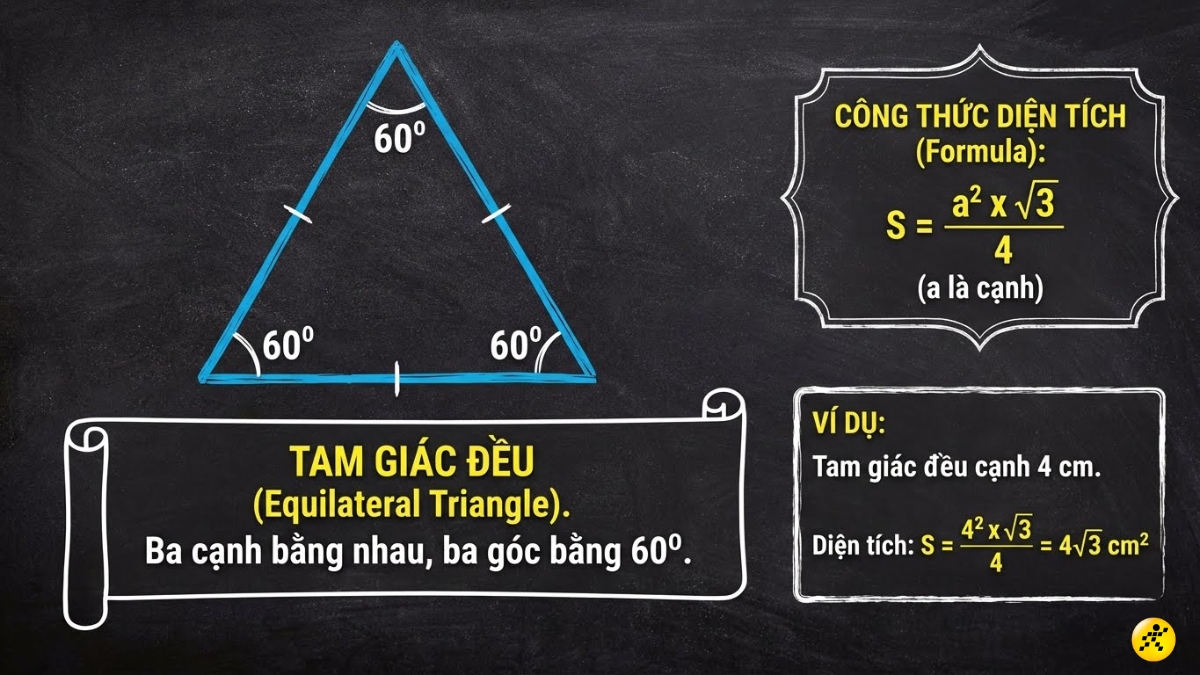
Công thức tam giác đều

Tam giác cân

Đối với tam giác cân, không có công thức tính nhanh riêng biệt. Bạn cần tìm chiều cao bằng cách áp dụng định lý Pythagoras rồi dùng công thức cơ bản.

Hướng dẫn: Kẻ đường cao từ đỉnh xuống cạnh đáy. Đường cao này sẽ chia cạnh đáy thành 2 đoạn bằng nhau. Áp dụng định lý Pythagoras trong tam giác vuông nhỏ vừa tạo để tìm chiều cao, sau đó tính diện tích như bình thường.

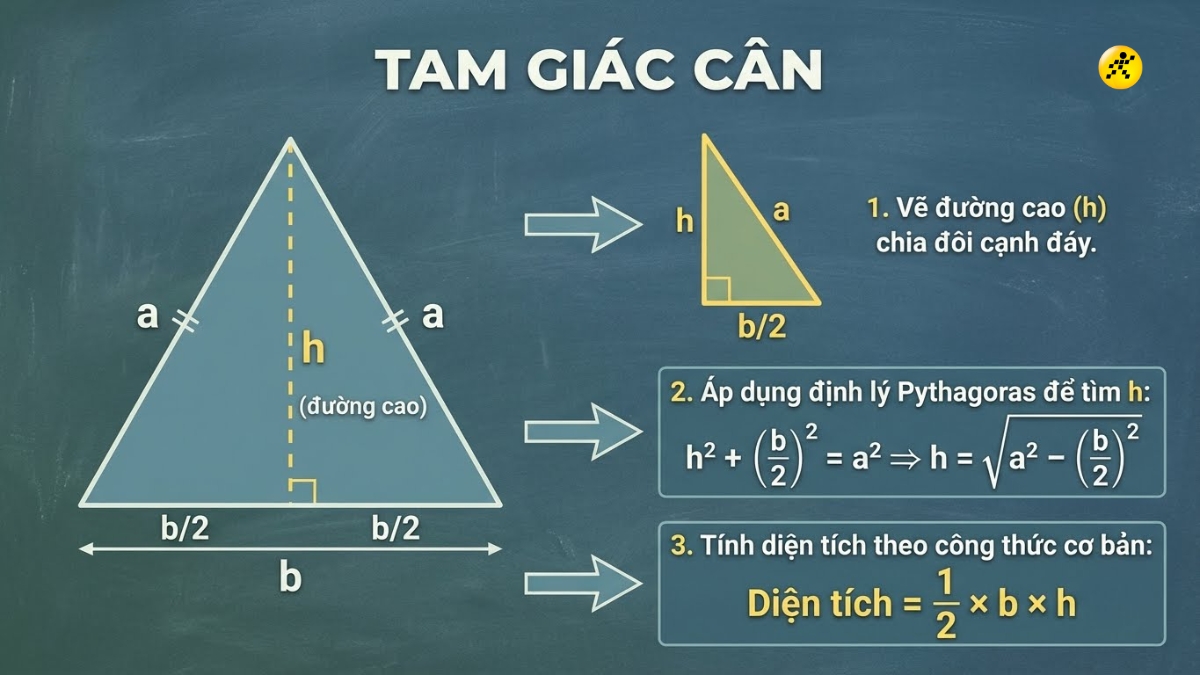
Công thức tam giác cân

6. Tính diện tích tam giác trong hệ tọa độ Oxyz

Trong chương trình hình học không gian, khi biết tọa độ 3 đỉnh của một tam giác, ta có thể tính diện tích của nó thông qua ứng dụng của tích có hướng của hai vector. Phương pháp này rất hữu ích trong các bài toán liên quan đến đồ họa máy tính và kỹ thuật.

Bước 1: Xác định tọa độ của 2 vector

Giả sử có 3 điểm A(x₁, y₁, z₁), B(x₂, y₂, z₂), C(x₃, y₃, z₃). Ta tính vector AB = (x₂ - x₁, y₂ - y₁, z₂ - z₁) và AC = (x₃ - x₁, y₃ - y₁, z₃ - z₁).

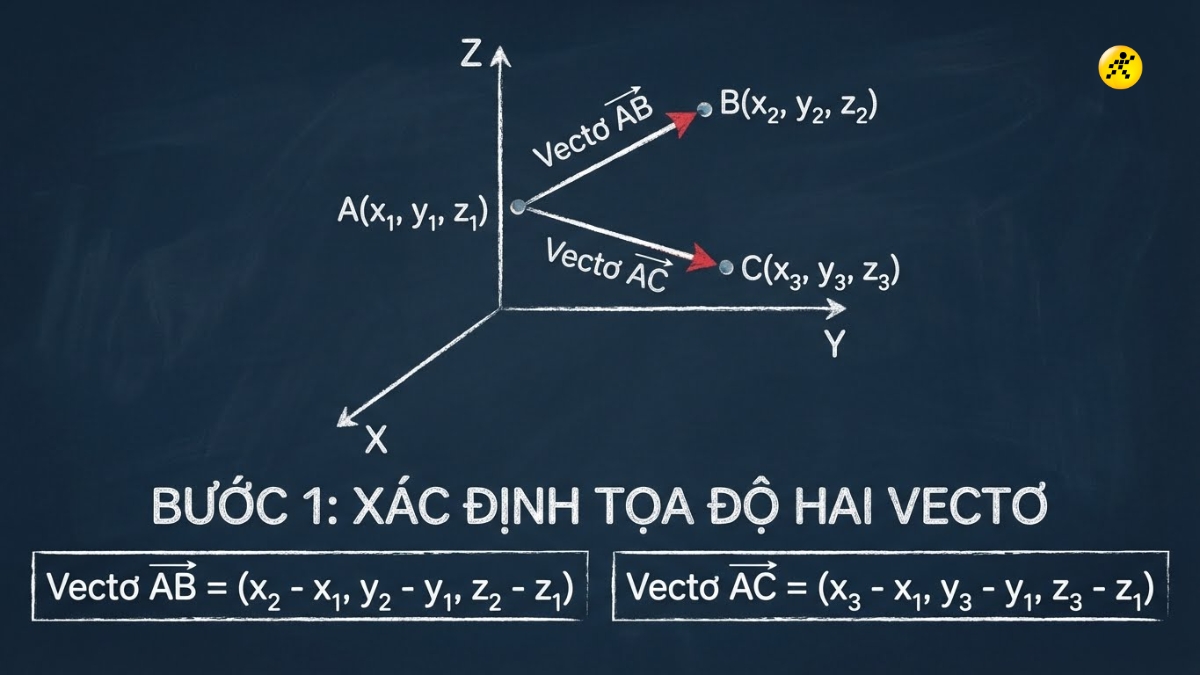
Xác định tọa độ của 2 vector

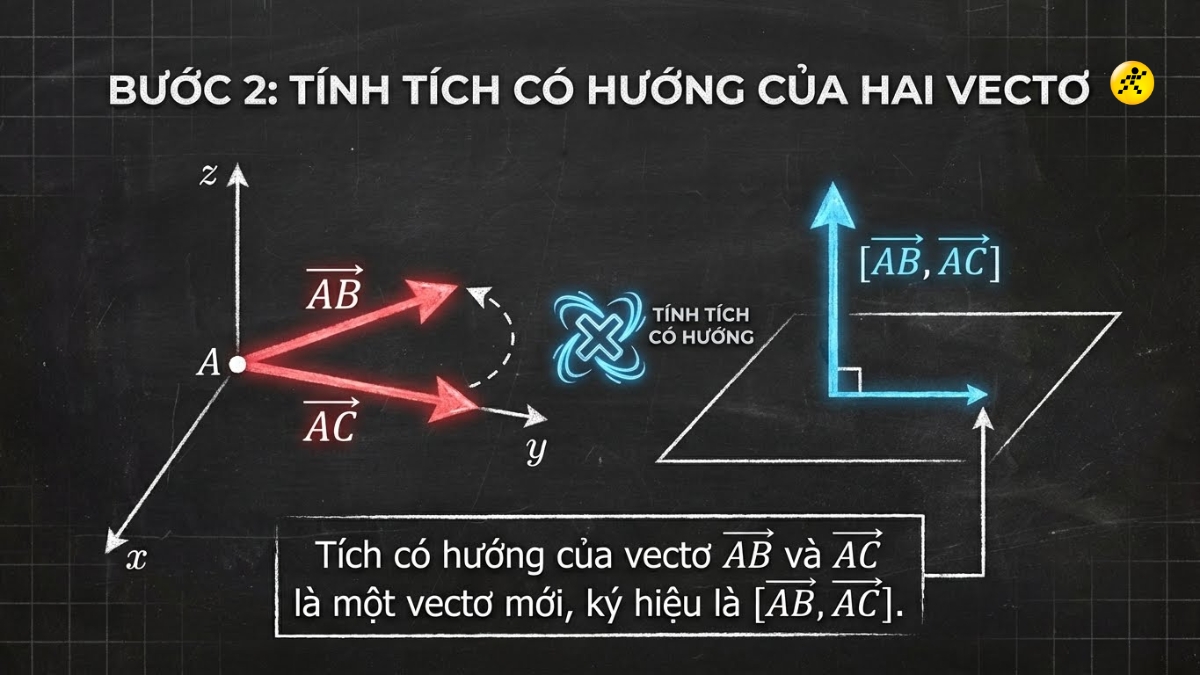
Bước 2: Tính tích có hướng của 2 vector

Tích có hướng của vector AB và AC là một vector mới, ký hiệu là [AB, AC]

Tính tích có hướng của 2 vector

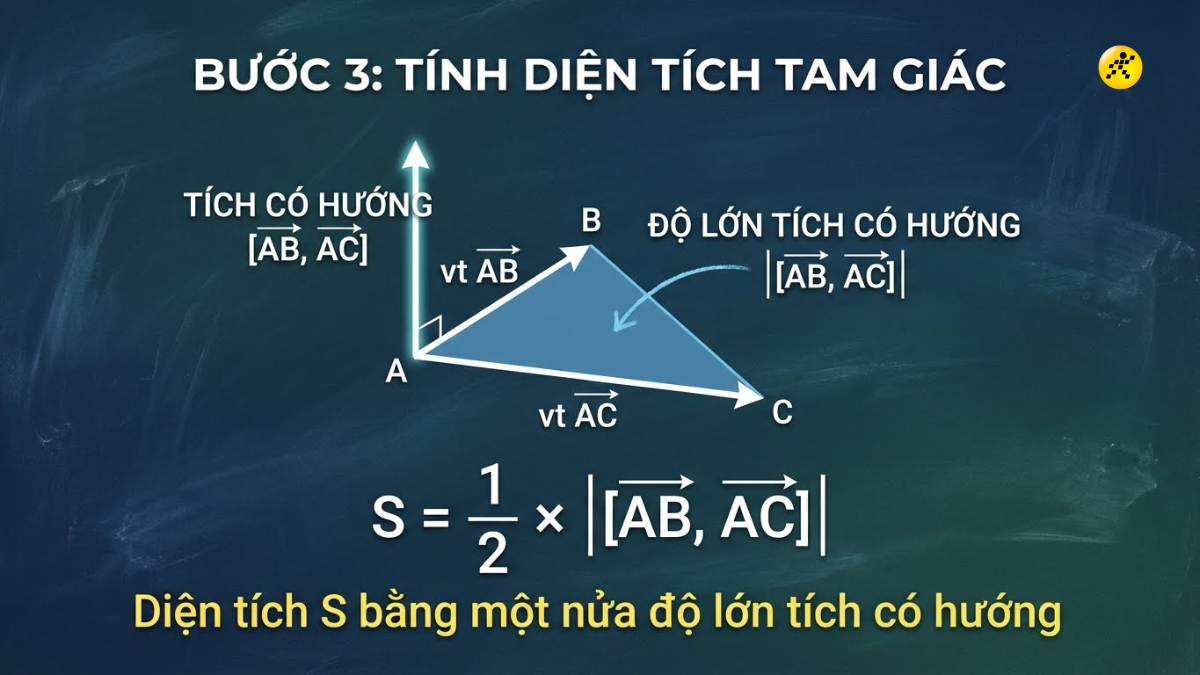
Bước 3: Tính diện tích

Diện tích tam giác bằng một nửa độ lớn của vector tích có hướng.

Công thức: S = 1/2 x |[AB, AC]|

Tính diện tích

Tham khảo ngay các mẫu máy tính bảng giúp bạn học tập và tra cứu công thức dễ dàng hơn:

Trả chậm 0%

iPad Pro M5 11 inch WiFi 256GB 29.990.000₫

Trả chậm 0% trả trước 0đ

Samsung Galaxy Tab A11+ 5G 8GB/256GB

8.690.000₫

9.190.000₫ -5%

Trả góp 0% trả trước 0đ

Samsung Galaxy Tab A11+ WiFi 6GB/128GB

6.190.000₫

6.690.000₫ -7%

Trả chậm 0% trả trước 0đ

OPPO Pad SE WiFi màn hình nhám 4GB/128GB

5.590.000₫

5.890.000₫ -5%

Trả chậm 0%

iPad A16 5G 128GB

12.990.000₫

13.990.000₫ -7%

Trả chậm 0%

iPad A16 WiFi 128GB

Online giá rẻ quá

8.690.000₫

9.790.000₫ -11%

Trả chậm 0% trả trước 0đ

OPPO Pad Neo WiFi 6GB/128GB

6.070.000₫

6.570.000₫ -7%

Trả chậm 0% trả trước 0đ

Samsung Galaxy Tab S10 Lite 5G 6GB/128GB

9.990.000₫

10.490.000₫ -4%

Trả chậm 0% trả trước 0đ

Samsung Galaxy Tab A11 4G 8GB/128GB

5.790.000₫

6.490.000₫ -10%

Xem thêm sản phẩm Máy tính bảng

7. Câu hỏi thường gặp về cách tính diện tích hình tam giác

Dưới đây là một số câu hỏi thường gặp có thể giúp bạn hiểu rõ hơn về các phương pháp tính diện tích hình tam giác.

Làm thế nào để tính chiều cao tam giác khi chỉ biết 3 cạnh?

Bạn có thể tính diện tích bằng công thức Heron trước, sau đó từ công thức S = 1/2 x a x h, bạn suy ra chiều cao h = 2S / a.

Đơn vị diện tích tam giác là gì?

Đơn vị diện tích là đơn vị vuông, ví dụ như mét vuông (m²), centimet vuông (cm²),... tùy thuộc vào đơn vị đo độ dài của các cạnh.

Công thức Heron có áp dụng cho tam giác vuông được không?

Có. Công thức Heron áp dụng được cho mọi loại tam giác, miễn là bạn biết độ dài của cả ba cạnh. Tuy nhiên, đối với tam giác vuông, sử dụng công thức 1/2 tích hai cạnh góc vuông sẽ nhanh hơn.

Để việc học tập và tính toán trở nên dễ dàng hơn, tham khảo ngay các mẫu laptop giá tốt:

Trả chậm 0%

MacBook Pro 14 inch M5 16GB/512GB 41.990.000₫

Trả chậm 0% trả trước 0đ

MacBook Air 13 inch M4 16GB/256GB

23.990.000₫

26.490.000₫ -9%

Trả chậm 0% trả trước 0đ

Dell 15 DC15250 i7 1355U (DC5I7748W1)

20.990.000₫

21.390.000₫

Trả chậm 0% trả trước 0đ

Lenovo IdeaPad Slim 3 15IRH10 i5 13420H (83K1000HVN)

15.890.000₫

16.990.000₫ -6%

Trả chậm 0% trả trước 0đ

Acer Aspire Lite 15 AL15 71P 517D i5 12450H (NX.J7KSV.001)

14.890.000₫

15.590.000₫

Trả chậm 0% trả trước 0đ

HP 15 fc0085AU R5 7430U (A6VV8PA)

14.590.000₫

15.790.000₫ -7%

Trả chậm 0% trả trước 0đ

Asus Vivobook Go 15 E1504FA R5 7520U (NJ776W)

13.590.000₫

14.190.000₫

Trả chậm 0%

MacBook Air 13 inch M2 16GB/256GB

19.690.000₫

24.490.000₫ -19%

Trả chậm 0% trả trước 0đ

Asus Gaming Vivobook 16X K3605VC i5 13420H (RP364W)

19.690.000₫

22.090.000₫ -10%

Xem thêm sản phẩm Laptop

Xem thêm:

Trên đây là tổng hợp đầy đủ các công thức tính diện tích hình tam giác phổ biến nhất. Hy vọng bài viết sẽ giúp bạn dễ dàng áp dụng vào việc học tập và giải quyết các bài toán thực tế. Chúc bạn thành công!

3 lượt xem

Từ khóa: cách tính diện tích hình tam giác, công thức tính diện tích hình tam giác, công thức tính diện tích hình tam giác, diện tích hình tam giác

Không tìm thấy kết quả phù hợp

Online giá rẻ quá

Online giá rẻ quá

Đặt câu hỏi