Tâm đối xứng là gì? Cách nhận biết, ứng dụng, bài tập chi tiết

Đóng góp bởi Dương Trúc Phương2 ngày trước

Tham khảo ngay các mẫu laptop có thiết kế đối xứng, tinh tế đang có giá tốt:

Trả chậm 0% trả trước 0đ

HP 15 fc0085AU R5 7430U (A6VV8PA)

14.290.000₫

16.090.000₫ -11%

Trả chậm 0%

MacBook Air 13 inch M2 16GB/256GB

19.690.000₫

24.490.000₫ -19%

Trả chậm 0% trả trước 0đ

MacBook Air 13 inch M4 16GB/256GB

23.990.000₫

26.490.000₫ -9%

Trả chậm 0% trả trước 0đ

Asus Vivobook Go 15 E1504FA R5 7520U (NJ776W)

13.390.000₫

14.190.000₫ -5%

Trả chậm 0% trả trước 0đ

Lenovo IdeaPad Slim 3 15IRH10 i5 13420H (83K1000HVN)

16.390.000₫

16.990.000₫

Trả chậm 0% trả trước 0đ

Lenovo Ideapad Slim 3 15AMN8 R5 7520U (82XQ00J0VN)

13.390.000₫

14.390.000₫ -6%

Trả chậm 0% trả trước 0đ

Asus Gaming Vivobook 16X K3605VC i5 13420H (RP364W)

19.690.000₫

22.090.000₫ -10%

Trả chậm 0% trả trước 0đ

HP 240 G10 i5 1334U (B93GZAT)

16.390.000₫

18.390.000₫ -10%

Trả chậm 0% trả trước 0đ

HP 15 fc0655AU R5 7430U (C81NGPA)

14.290.000₫

16.090.000₫ -11%

Xem thêm sản phẩm Laptop

Tâm đối xứng là khái niệm hình học cơ bản có ứng dụng lớn trong thiết kế laptop. Bài viết này sẽ giúp bạn hiểu rõ định nghĩa tâm đối xứng và cách phân biệt nó với trục đối xứng. Khám phá ngay!

1. Tâm đối xứng là gì?

Tâm đối xứng (O) là một điểm mà khi quay một hình đối xứng qua điểm đó 180 độ (nửa vòng tròn), hình thu được sẽ trùng khít lên vị trí ban đầu của nó; hoặc nói cách khác, điểm đối xứng của mọi điểm thuộc hình qua (O) cũng phải thuộc hình đó.

Tâm đối xứng giúp nhận diện các hình có tính chất đặc biệt như đoạn thẳng (trung điểm), hình bình hành (giao điểm hai đường chéo), hình tròn (tâm), hoặc một số chữ cái như 'H', 'I', 'N', 'O', 'S', 'X', 'Z.

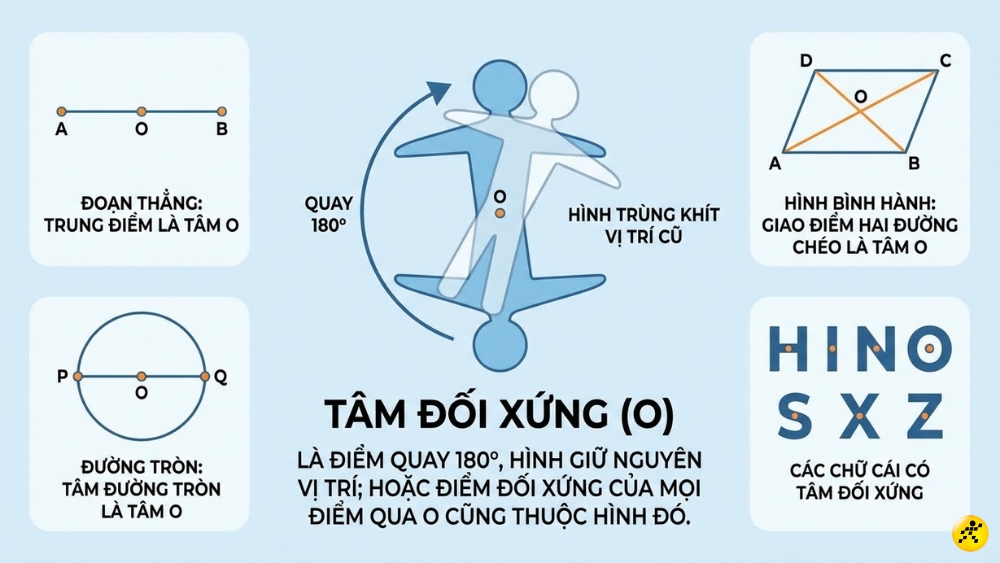
Tâm đối xứng (O)

Tính chất cốt lõi: Tâm đối xứng O luôn đóng vai trò là trung điểm của mỗi đoạn thẳng nối hai điểm tương ứng đối xứng với nhau qua nó trên cùng một hình. Đây là đặc điểm then chốt để các nhà thiết kế tính toán độ cân bằng cho các sản phẩm vật lý.

2. Phân biệt tâm đối xứng và trục đối xứng

Nhiều người thường nhầm lẫn giữa hai khái niệm này vì chúng đều tạo ra sự cân đối. Tuy nhiên, về bản chất hình học, chúng có những sự khác biệt rất rõ rệt:

Tiêu chí	Tâm đối xứng	Trục đối xứng
Bản chất	Là một điểm duy nhất.	Là một đường thẳng (có thể có nhiều đường).
Phép biến hình	Thực hiện phép quay 180 độ quanh điểm đó.	Thực hiện phép lật (gấp) qua đường thẳng đó.
Cách nhận biết	Hình sau khi quay trùng khít với hình ban đầu.	Nửa hình bên này sau khi lật sẽ trùng khít với nửa hình bên kia.
Ví dụ điển hình	Tâm của hình tròn, giao điểm 2 đường chéo hình vuông.	Đường kính của hình tròn, đường trung trực của tam giác cân.

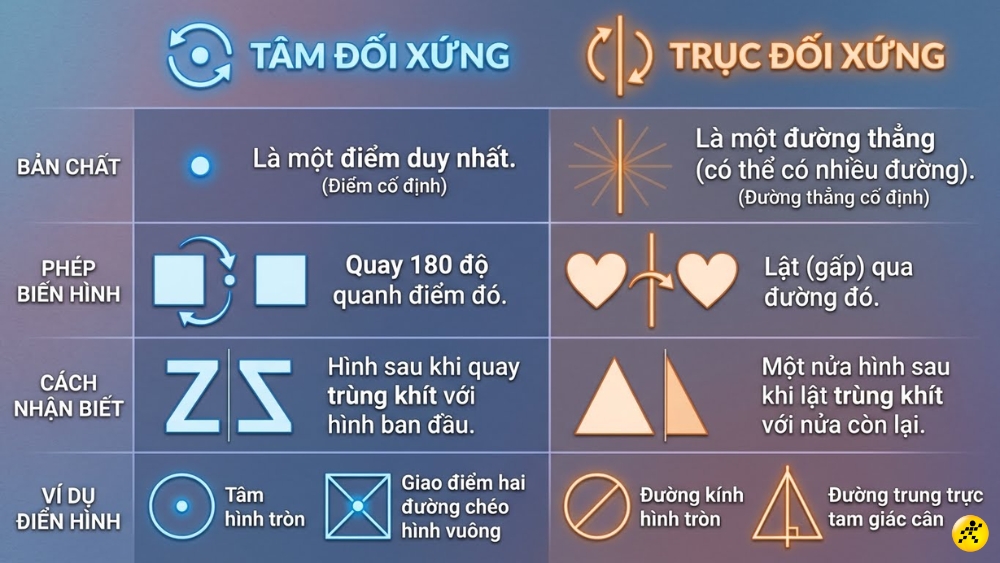
Phân biệt tâm đối xứng và trục đối xứng

Lưu ý quan trọng: Một hình có thể sở hữu tâm đối xứng nhưng lại không có bất kỳ trục đối xứng nào (như hình bình hành thông thường). Ngược lại, có những hình cực cân đối như tam giác đều nhưng lại không có tâm đối xứng.

3. Các hình có tâm đối xứng thường gặp

Trong chương trình học và thực tế đời sống, bạn sẽ thường xuyên bắt gặp các hình có tâm đối xứng sau:

Đoạn thẳng: Tâm đối xứng chính là trung điểm của đoạn thẳng đó.
Hình tròn: Tâm của hình tròn chính là tâm đối xứng duy nhất.
Hình bình hành: Tâm đối xứng là giao điểm của hai đường chéo.
Hình chữ nhật, hình thoi, hình vuông: Tâm đối xứng là giao điểm hai đường chéo.
Lục giác đều: Giao điểm của các đường chéo chính là tâm đối xứng.
Chữ cái in hoa: Một số chữ cái như H, I, N, O, S, X, Z có cấu trúc đối xứng tâm rõ rệt.

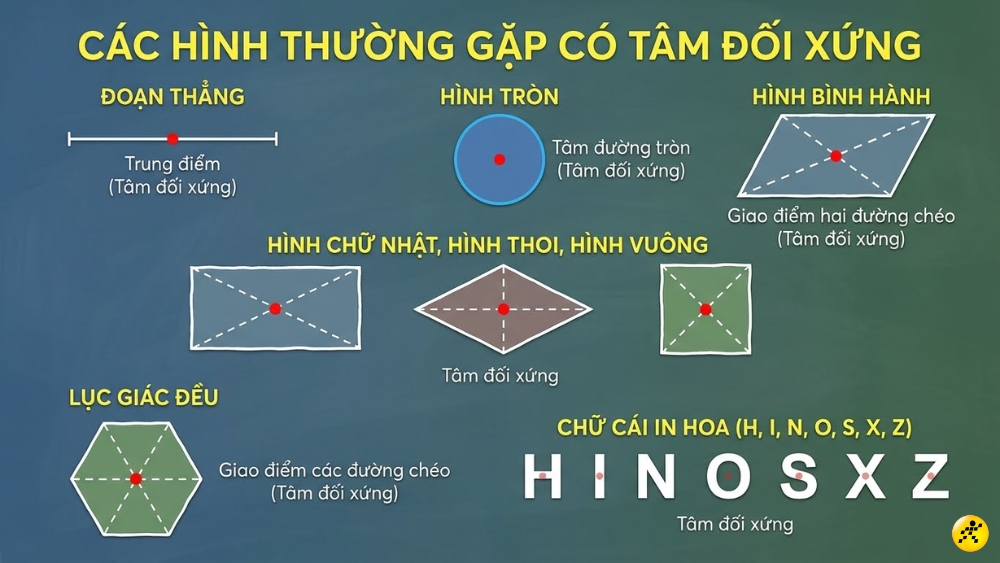
Các hình có tâm đối xứng thường gặp

4. Các hình không có tâm đối xứng

Không phải mỗi hình dạng cân đối đều có tâm đối xứng. Việc nhận biết các hình không có tính chất này giúp chúng ta ứng dụng chính xác hơn trong thiết kế:

Hình tam giác: Tất cả các loại tam giác (đều, cân, vuông hay thường) đều không có tâm đối xứng.
Hình thang: Bao gồm cả hình thang cân, chúng chỉ có trục đối xứng chứ không có tâm đối xứng.
Ngũ giác đều: Các đa giác đều có số cạnh lẻ (như ngũ giác, thất giác) sẽ không có tâm đối xứng.
Phần lớn các chữ cái và chữ số còn lại: Ví dụ chữ A, chữ M, chữ E...

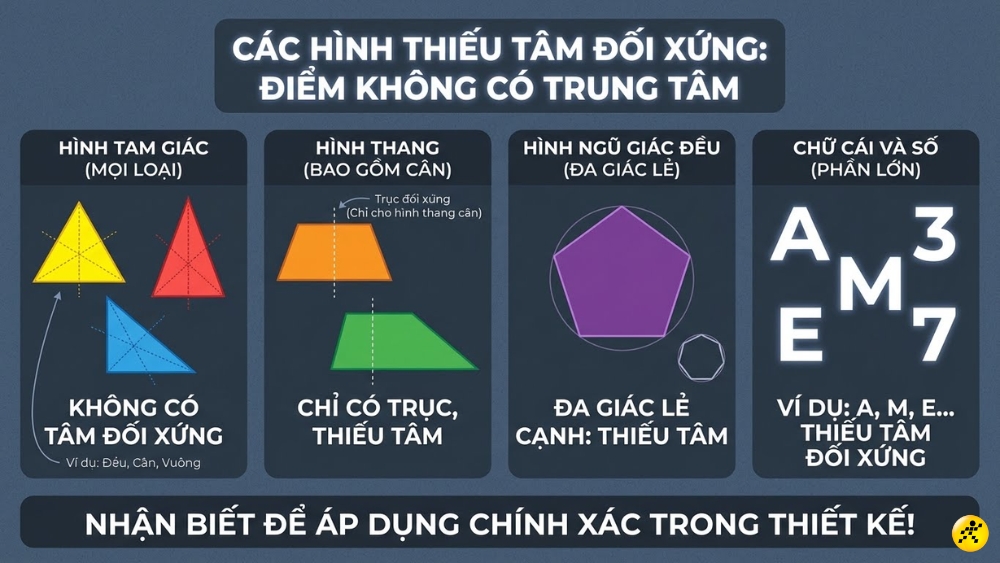
Các hình không có tâm đối xứng

5. Các dạng bài tập về tâm đối xứng kèm lời giải

Các dạng bài tập về tâm đối xứng thường gặp trong chương trình Toán 6 - 8, tập trung vào nhận biết, tính khoảng cách và tọa độ. Dưới đây là các dạng chính kèm lời giải chi tiết:

Nhận biết tâm đối xứng

Xác định hai điểm/hình đối xứng qua điểm O (O là trung điểm).

Bài tập: Cho đoạn AB = 6cm, O là tâm đối xứng. Tính OA.

Lời giải: OA = OB = AB/2 = 6/2 = 3cm. O chia AB thành hai phần bằng nhau.

Tính độ dài đoạn đối xứng

Dùng tính chất: đoạn đối xứng qua O bằng nhau.

Bài tập: Trong tam giác ABC, BC = 22cm. M, N là trung điểm AB, AC. O là tâm đối xứng của MN. Tính M'N'.

Lời giải: MN = 22 - 8 - 4 = 10cm. Do đó M'N' = MN = 10cm.

Tọa độ điểm đối xứng

Tìm ảnh A'(x',y') của A(x,y) qua O(a,b): x' = 2a - x, y' = 2b - y.

Bài tập: Tìm ảnh của A(3,4) qua O(1,2).

Lời giải: x' = 2×1 - 3 = -1, y' = 2×2 - 4 = 0. A'(-1,0).

Chọn phát biểu đúng

Nhận diện tính chất hình học đối xứng tâm.

Bài tập: Chọn đúng: A. Hai đoạn đối xứng qua O bằng nhau. B. Hai góc đối xứng qua O bằng nhau.

Lời giải: Đúng cả A và B. Tam giác, hình bình hành cũng có tính chất tương tự.

Bài toán hình có tâm đối xứng

Tìm tâm O của hình vuông, hình thoi, tròn.

Bài tập: Cho hình bình hành ABCD có tâm O. E trên OD. F là ảnh của C qua E. EF song song AD?

Lời giải: Có. Vì phép đối xứng tâm bảo toàn song song và bằng nhau.[

6. Ứng dụng của tâm đối xứng trong thiết kế công nghệ

Nguyên lý đối xứng tâm không chỉ là kiến thức trên sách vở mà là "kim chỉ nam" trong thiết kế công nghiệp. Nó mang lại cảm giác cân bằng, hài hòa và chuyên nghiệp cho các sản phẩm công nghệ cao.

Thiết kế laptop tổng thể: Các dòng máy tính xách tay hiện nay thường ưu tiên thiết kế đối xứng qua tâm (điểm chính giữa máy).

Bạn sẽ dễ dàng nhận thấy logo của hãng sản xuất thường được đặt chính xác tại tâm đối xứng của mặt lưng máy. Việc này không chỉ tạo điểm nhấn thẩm mỹ mà còn giúp người dùng cảm nhận được sự ổn định về mặt thị giác khi đóng mở máy.

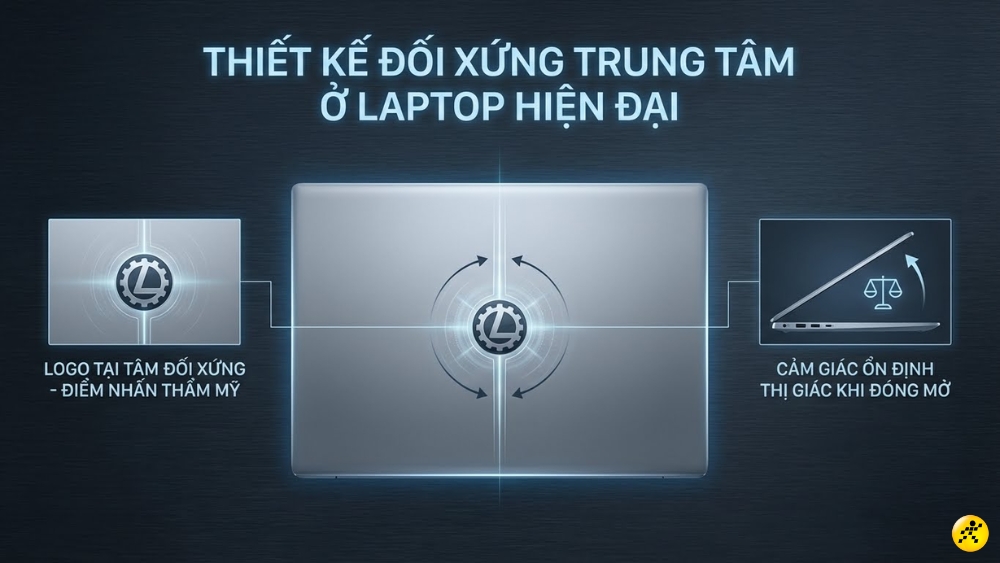
Thiết kế laptop đối xứng

Tham khảo ngay các mẫu laptop có thiết kế đối xứng, tinh tế đang có giá tốt:

Trả chậm 0% trả trước 0đ

HP 15 fc0085AU R5 7430U (A6VV8PA)

14.290.000₫

16.090.000₫ -11%

Trả chậm 0%

MacBook Air 13 inch M2 16GB/256GB

19.690.000₫

24.490.000₫ -19%

Trả chậm 0% trả trước 0đ

MacBook Air 13 inch M4 16GB/256GB

23.990.000₫

26.490.000₫ -9%

Trả chậm 0% trả trước 0đ

Asus Vivobook Go 15 E1504FA R5 7520U (NJ776W)

13.390.000₫

14.190.000₫ -5%

Trả chậm 0% trả trước 0đ

Lenovo IdeaPad Slim 3 15IRH10 i5 13420H (83K1000HVN)

16.390.000₫

16.990.000₫

Trả chậm 0% trả trước 0đ

Lenovo Ideapad Slim 3 15AMN8 R5 7520U (82XQ00J0VN)

13.390.000₫

14.390.000₫ -6%

Trả chậm 0% trả trước 0đ

Asus Gaming Vivobook 16X K3605VC i5 13420H (RP364W)

19.690.000₫

22.090.000₫ -10%

Trả chậm 0% trả trước 0đ

HP 240 G10 i5 1334U (B93GZAT)

16.390.000₫

18.390.000₫ -10%

Trả chậm 0% trả trước 0đ

HP 15 fc0655AU R5 7430U (C81NGPA)

14.290.000₫

16.090.000₫ -11%

Xem thêm sản phẩm Laptop

Thiết kế điện thoại: Mặt lưng của nhiều mẫu smartphone hiện đại áp dụng triệt để nguyên tắc này.

Cụm camera, cảm biến vân tay hoặc logo thương hiệu thường được bố trí nằm trên trục dọc đi qua tâm hoặc sắp xếp cân xứng quanh một tâm điểm, tạo nên vẻ ngoài sang trọng.

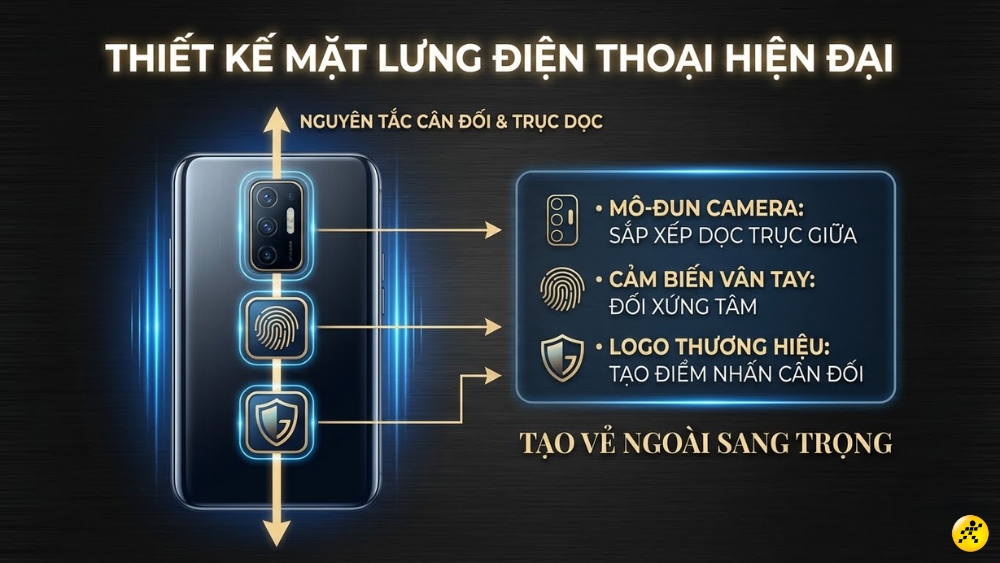
Thiết kế điện thoại

Khám phá các mẫu điện thoại với thiết kế đối xứng, sang trọng tại TGDĐ:

Trả góp 0%

iPhone 17 Pro Max 256GB 37.990.000₫

Trả chậm 0% trả trước 0đ

OPPO A6 Pro 8GB/128GB 8.290.000₫

Trả chậm 0%

iPhone 16 Pro Max 256GB

31.590.000₫

33.990.000₫ -7%

Trả chậm 0% trả trước 0đ

OPPO Reno14 F 5G 12GB/256GB 11.290.000₫

Trả chậm 0% trả trước 0đ

OPPO A5x 4GB/128GB 4.220.000₫

Trả chậm 0% trả trước 0đ

OPPO A5 6GB/128GB 5.290.000₫

Trả chậm 0% trả trước 0đ

Xiaomi Redmi Note 14 Pro 5G 8GB/256GB

Online giá rẻ quá

7.720.000₫

9.320.000₫ -17%

Trả chậm 0% trả trước 0đ

Xiaomi Redmi Note 14 Pro 8GB/256GB

5.400.000₫

7.850.000₫ -31%

Trả chậm 0% trả trước 0đ

Samsung Galaxy A07 6GB/128GB

3.490.000₫

3.690.000₫ -5%

Xem thêm sản phẩm Điện thoại

Công nghệ hiện đại như eSIM cũng giúp việc thiết kế các thiết bị trở nên đối xứng hơn vì loại bỏ được khe cắm vật lý chiếm diện tích.

Ngoài ra, trong các phần mềm báo cáo, việc sử dụng Pivot table cũng yêu cầu sự cân đối trong cách bố trí dữ liệu để người dùng dễ dàng theo dõi.

Công nghệ hiện đại

7. Câu hỏi thường gặp về tâm đối xứng

Hình vuông có mấy tâm đối xứng?

Mỗi hình vuông chỉ có duy nhất một tâm đối xứng, đó là giao điểm của hai đường chéo. Tuy nhiên, hình vuông lại có tới 4 trục đối xứng.

Làm sao để xác định nhanh tâm đối xứng của một đa giác?

Nếu đa giác đó là đa giác đều và có số cạnh chẵn (như lục giác đều, bát giác đều), tâm đối xứng chính là tâm đường tròn ngoại tiếp đa giác đó.

Đồ thị hàm số nào có tâm đối xứng?

Trong giải tích, đồ thị của các hàm số lẻ (như y = x^3, y = sin x) luôn nhận gốc tọa độ O (0,0) làm tâm đối xứng. Đối với hàm bậc ba tổng quát, tâm đối xứng chính là điểm uốn của đồ thị.

Có thể bạn quan tâm đến các mẫu màn hình máy tính với thiết kế hiện đại đối xứng đẹp mắt:

Xiaomi 27 inch Full HD A27i

Online giá rẻ quá

2.340.000₫

2.990.000₫ -21%

Samsung S3 S30GD 27 inch Full HD LS27D300GAEXXV

Online giá rẻ quá

2.690.000₫

3.090.000₫ -12%

MSI PRO 24.5 inch Full HD MP252L

1.790.000₫

2.190.000₫ -18%

SingPC 21.5 inch Full HD P22F100-IPS

1.290.000₫

1.590.000₫ -18%

Samsung S3 S30GD 23.8 inch Full HD LS24D300GAEXXV

2.290.000₫

2.490.000₫ -8%

MSI 24.5 inch Full HD MP251 E2

Online giá rẻ quá

2.190.000₫

2.590.000₫ -15%

Asus Gaming TUF 27 inch Full HD VG279Q3R

2.790.000₫

3.190.000₫ -12%

MSI PRO 21.45 inch Full HD MP223 E2

1.590.000₫

1.890.000₫ -15%

MSI PRO 27 inch Full HD MP272LKL

2.290.000₫

2.690.000₫ -14%

Xem thêm sản phẩm Màn hình máy tính

Xem thêm:

Tâm đối xứng là một khái niệm hình học cốt lõi tạo nên sự cân bằng cho các thiết bị như màn hình máy tính và laptop. Cảm ơn bạn đã theo dõi bài viết này!

8 lượt xem

Từ khóa: tâm đối xứng là gì, tâm đối xứng

Không tìm thấy kết quả phù hợp

Online giá rẻ quá

Online giá rẻ quá

Online giá rẻ quá

Online giá rẻ quá

Đặt câu hỏi